题目内容
2位男生和3位女生共5位同学站成一排,若两男生必须相邻,则不同排法的种数是( )
| A、60 | B、48 | C、42 | D、36 |
考点:计数原理的应用
专题:排列组合
分析:利用捆绑法,把两男生捆绑在一起看作一个元素,和3位女生进行全排列,问题得以解决.
解答:
解:利用捆绑法,把两男生捆绑在一起看作一个元素有
种,和3位女生进行全排列有
,则不同排法的种数共有
=48.
故选B.
| A | 2 2 |
| A | 4 4 |
| A | 2 2 |
| •A | 4 4 |
故选B.
点评:本题考查了分步计数原理,利用捆绑法,把相邻的元素捆绑在一起,再和另外的元素全排.

练习册系列答案
相关题目
对于函数f(x),若存在区间M=[a,b],(a<b),使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的一个“稳定区间”,现有四个函数:
①f(x)=x2;
②f(x)=sin(
x);
③f(x)=lnx
④f(x)=x3-3x
其中存在“稳定区间”的函数为( )
①f(x)=x2;
②f(x)=sin(
| π |
| 2 |
③f(x)=lnx
④f(x)=x3-3x
其中存在“稳定区间”的函数为( )
| A、① | B、①② | C、①②③ | D、①②④ |
直线xcosθ+ysinθ-2=0与圆(x-sinθ)2+(y-2cosθ)2=
(θ∈R)的位置关系为( )
| 1 |
| 4 |
| A、相交,相切或相离 |
| B、相切 |
| C、相切或相离 |
| D、相交或相切 |
一个长方体被一平面截去一部分所得几何体的三视图如图,则该几何体的体积是( )


| A、1440 | B、1200 |
| C、960 | D、720 |
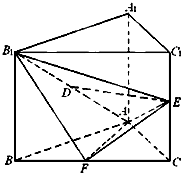 已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.