题目内容
某单位有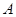 、
、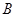 、
、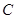 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点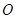 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为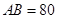
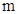 ,
,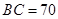
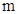 ,
,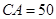
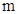 .假定
.假定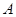 、
、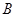 、
、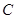 、
、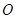 四点在同一平面内.
四点在同一平面内.
(Ⅰ)求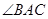 的大小;
的大小;
(Ⅱ)求点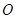 到直线
到直线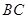 的距
的距
(1) (2)
(2)
解析试题分析:(1). 在 中,知道三条边长利用余弦定理
中,知道三条边长利用余弦定理 能够求出
能够求出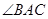 的大小.(Ⅱ).因为点O到三个顶点的距离相等,所以O为
的大小.(Ⅱ).因为点O到三个顶点的距离相等,所以O为 的外接圆的圆心,由正弦定理
的外接圆的圆心,由正弦定理 能够求出外接圆的半径.
能够求出外接圆的半径. 在由勾股定理求出O到BC的距离
在由勾股定理求出O到BC的距离
 .
.
试题解析:解:(Ⅰ)在△ 中,因为
中,因为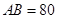
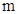 ,
,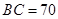
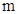 ,
,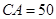
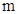 ,
,
由余弦定理得
 .
.
因为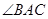 为△
为△ 的内角,所以
的内角,所以 . 5分
. 5分
(Ⅱ)方法1:设外接圆的半径为 ,
,
因为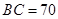 ,由(1)知
,由(1)知 ,所以
,所以 .
.
所以 ,即
,即 .
.
过点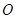 作边
作边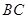 的垂线,垂足为
的垂线,垂足为 ,
,
在△ 中,
中, ,
, ,
,
所以
 .
.
所以点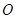 到直线
到直线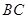 的距离为
的距离为
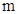 .
.
考点:余弦定理、正弦定理

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 ,已知
,已知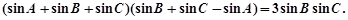
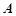 值;
值; 的最大值.
的最大值.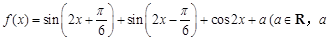 为常数).
为常数).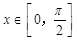 时,
时,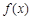 的最小值为– 2 ,求a的值.
的最小值为– 2 ,求a的值.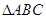 中,内角
中,内角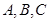 所对边长分别为
所对边长分别为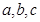 ,
,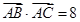 ,
,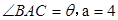 。
。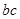 的最大值; (2)求函数
的最大值; (2)求函数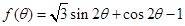 的值域.
的值域.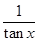 )sin2x+msin(x+
)sin2x+msin(x+ )sin(x-
)sin(x-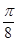 ,
, ]上的取值范围;
]上的取值范围;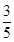 ,求m的值.
,求m的值.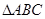 中,角
中,角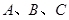 所对的边为
所对的边为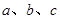 ,且满足
,且满足
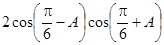
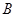 的值;
的值;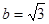 且
且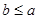 ,求
,求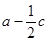 的取值范围.
的取值范围.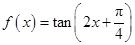 .
.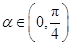 ,若
,若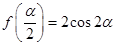 ,求
,求 的大小.
的大小.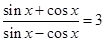
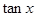 的值;
的值; 是第三象限的角,化简三角式
是第三象限的角,化简三角式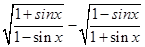 ,并求值.
,并求值.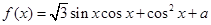 .
. 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;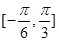 上的最大值与最小值的和为
上的最大值与最小值的和为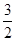 ,求
,求 的值.
的值.