题目内容
在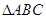 中,内角
中,内角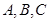 所对边长分别为
所对边长分别为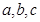 ,
,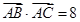 ,
,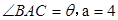 。
。
(1)求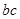 的最大值; (2)求函数
的最大值; (2)求函数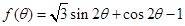 的值域.
的值域.
(1)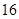 ; (2)
; (2)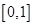 .
.
解析试题分析:(1)由数量积的定义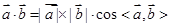 ,又在
,又在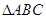 中,可得到
中,可得到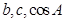 之间的一个等式,又由
之间的一个等式,又由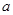 已知,可想到运用余弦定理
已知,可想到运用余弦定理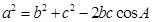 ,可找出
,可找出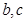 之间满足的等式关系,最后运用基本不等式
之间满足的等式关系,最后运用基本不等式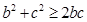 ,就可求出
,就可求出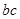 的最大值; (2)对题中所给函数
的最大值; (2)对题中所给函数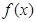 运用公式
运用公式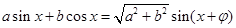 进行化简,可得
进行化简,可得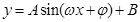 的形式,结合中所求
的形式,结合中所求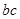 的最大值,进而求出
的最大值,进而求出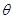 的范围,最后借助三角函数图象求出函数的最大值和最小值.
的范围,最后借助三角函数图象求出函数的最大值和最小值.
试题解析:(1)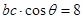 ,
, 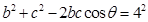 即
即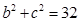 2分
2分
又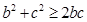 所以
所以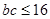 ,即
,即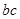 的最大值为
的最大值为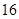 4分
4分
当且仅当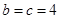 ,
,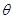
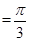 时取得最大值 5分
时取得最大值 5分
(2)结合(1)得, , 所以
, 所以 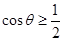 ,
,
又0<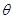 <
<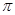 所以0<
所以0<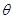
 7分
7分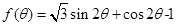
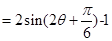 8分
8分
因0<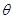
 ,所以
,所以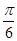 <
<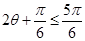 ,
, 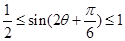 9分
9分
当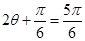 即
即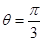 时,
时,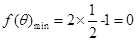 10分
10分
当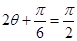 即
即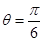 时,
时,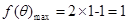 11分
11分
所以,函数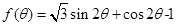 的值域为
的值域为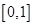 12分
12分
考点:1.向量的数量积;2.余弦定理;3.三角函数的图象和性质

练习册系列答案
相关题目

 按第一列展开得
按第一列展开得 ,记函数
,记函数 ,且
,且 的最大值是
的最大值是 .
. ;
; 的图像向左平移
的图像向左平移 个单位,再将所得图像上各点的横坐标扩大为原来的
个单位,再将所得图像上各点的横坐标扩大为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 的图像,求
的图像,求 在
在 上的值域.
上的值域. 上的一点,以
上的一点,以 轴的非负半轴为始边、OP为终边的角记为
轴的非负半轴为始边、OP为终边的角记为 ,又向量
,又向量 。且
。且 .
. 的单调减区间;
的单调减区间; 的方程
的方程 在
在 内有两个不同的解,求
内有两个不同的解,求 的取值范围.
的取值范围.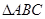 中,三条边
中,三条边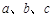 所对的角分别为
所对的角分别为 、
、 、
、 ,且
,且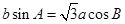 .
.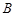 的大小;
的大小;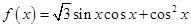 ,求
,求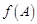 的最大值.
的最大值.  =
= -sin(2x-
-sin(2x- ).
).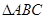 的内角
的内角 的对边分别为
的对边分别为 ,
, ,f(
,f( )=
)= ,若
,若 ,求
,求 ,
, ,
,
 ,求向量
,求向量 、
、 的夹角;
的夹角; 时,求函数
时,求函数 的最大值.
的最大值.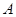 、
、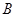 、
、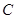 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点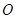 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为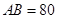
 ,
,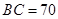
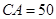
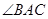 的大小;
的大小;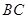 的距
的距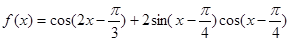 (
(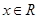 ).
). 的最小正周期;
的最小正周期;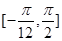 上的值域.
上的值域. 中,
中, 的对边分别为
的对边分别为 且
且 成等差数列.
成等差数列. 的范围.
的范围.