题目内容
已知函数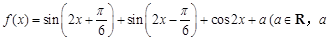 为常数).
为常数).
(Ⅰ)求函数的最小正周期;
(Ⅱ)求函数的单调递增区间;
(Ⅲ)若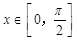 时,
时,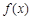 的最小值为– 2 ,求a的值.
的最小值为– 2 ,求a的值.
(Ⅰ)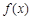 的最小正周期
的最小正周期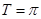 ;(Ⅱ)函数的单调递增区间
;(Ⅱ)函数的单调递增区间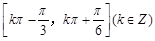 ;(Ⅲ)
;(Ⅲ)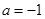 .
.
解析试题分析:(Ⅰ)求函数的最小正周期,由函数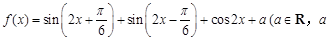 为常数),通过三角恒等变化,把它转化为一个角的一个三角函数,从而可求函数的最小正周期;(Ⅱ)求函数的单调递增区间,可由
为常数),通过三角恒等变化,把它转化为一个角的一个三角函数,从而可求函数的最小正周期;(Ⅱ)求函数的单调递增区间,可由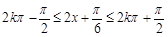 ,解出
,解出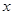 的范围即可,注意不要忽略
的范围即可,注意不要忽略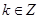 这个条件;(Ⅲ)利用三角函数的图像,及
这个条件;(Ⅲ)利用三角函数的图像,及 ,可求出
,可求出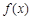 的最小值,让最小值等于
的最小值,让最小值等于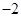 ,可求出a的值.
,可求出a的值.
试题解析: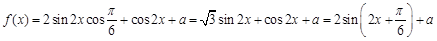
∴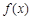 的最小正周期
的最小正周期
(Ⅱ)当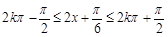 即
即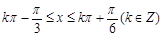 时,函数
时,函数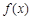 单调递增,故所求区间为
单调递增,故所求区间为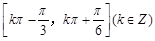
(Ⅲ)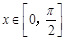 时,
时,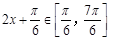
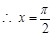 时,
时,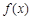 取得最小值
取得最小值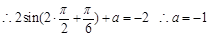
考点:三角函数的性质.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 .
. 在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);

 时,求函数
时,求函数 的值.
的值. (
( )的最小正周期为
)的最小正周期为 .
. 的单调增区间;
的单调增区间; 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数 的图象.求
的图象.求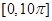 上零点的个数.
上零点的个数. 上的一点,以
上的一点,以 轴的非负半轴为始边、OP为终边的角记为
轴的非负半轴为始边、OP为终边的角记为 ,又向量
,又向量 。且
。且 .
. 的单调减区间;
的单调减区间; 的方程
的方程 在
在 内有两个不同的解,求
内有两个不同的解,求 的取值范围.
的取值范围. 是关于x的方程x2-kx+k2-3=0的两实根,且3π<α<
是关于x的方程x2-kx+k2-3=0的两实根,且3π<α< π,
π,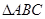 中,三条边
中,三条边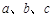 所对的角分别为
所对的角分别为 、
、 、
、 ,且
,且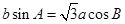 .
.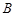 的大小;
的大小;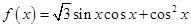 ,求
,求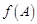 的最大值.
的最大值.  =
= -sin(2x-
-sin(2x- ).
).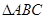 的内角
的内角 的对边分别为
的对边分别为 ,
, ,f(
,f( )=
)= ,若
,若 ,求
,求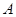 、
、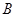 、
、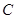 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点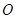 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为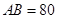
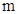 ,
,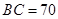
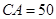
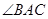 的大小;
的大小;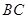 的距
的距 中,
中,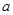 、
、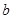 、
、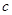 是三个内角
是三个内角 、
、 、
、 的对边,关于
的对边,关于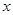 的不等式
的不等式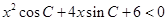
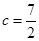 ,
,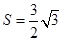 ,求当角
,求当角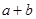 的值.
的值.