题目内容
10.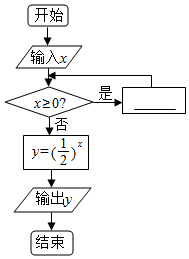 已知①x=x-1,②x=x-2,③x=x-3,④x=x-4在如图所示的程序框图中,如果输入x=10,而输出y=4,则在空白处可填入( )
已知①x=x-1,②x=x-2,③x=x-3,④x=x-4在如图所示的程序框图中,如果输入x=10,而输出y=4,则在空白处可填入( )| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ②③④ |
分析 先根据输出的y值,确定跳出循环的x值,依次判断当“?”处填①②③④时是否满足,可得答案.
解答 解:由y=($\frac{1}{2}$)x=4⇒x=-2,
∴输入x=10,当“?”处填①时,跳出循环x=-1,∴①错误;
当“?”处填②时,跳出循环x=-2,∴②正确;
当“?”处填③时,跳出循环x=-2,∴③正确;
当“?”处填④时,跳出循环x=-2,∴④正确.
故选:D.
点评 本题考查了当型循环结构的程序框图,根据框图的流程确定跳出循环的x值是解题的关键,属于基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
5.从某大学随机抽取的5名女大学生的身高x(厘米)和体重y(公斤)数据如表
根据上表可得回归直线方程为$\hat y=0.92x+\hat a$,则$\hat a$=( )
| x | 165 | 160 | 175 | 155 | 170 |
| y | 58 | 52 | 62 | 43 | 60 |
| A. | -104.4 | B. | 104.4 | C. | -96.8 | D. | 96.8 |
2.若${y^3}{(x+\frac{1}{xy})^n}(n∈{N^*})$的展开式中存在常数项,则常数项为( )
| A. | 15 | B. | 20 | C. | 30 | D. | 120 |
20.已知集合A={2,3},B={x|(x-2)(x+2)=0},则A∪B=( )
| A. | ∅ | B. | {2} | C. | {2,3} | D. | {-2,2,3} |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示. 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD⊥DC,DC∥AB,PA=AB=2,BC=$\sqrt{2}$,AD=DC=1.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD⊥DC,DC∥AB,PA=AB=2,BC=$\sqrt{2}$,AD=DC=1.