题目内容
6.证明平行六面体的对角线交于一点,并且在交点处互相平分.分析 在平行六面体ABCD-A′B′C′D′中,设O、P、M、N分别是AC′、BD′、CA′、DB′的中点,推导出$\overrightarrow{AO}$=$\overrightarrow{AP}$=$\overrightarrow{AM}$=$\overrightarrow{AN}$=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{'}})$,由此能证明对角线AC′、BD′、CA′、DB′交于一点,且在交点处互相平分.
解答  已知平行六面体ABCD-A′B′C′D′,求证:对角线AC′、BD′、CA′、DB′交于一点,且在交点处互相平分.
已知平行六面体ABCD-A′B′C′D′,求证:对角线AC′、BD′、CA′、DB′交于一点,且在交点处互相平分.
证明:如图,在平行六面体ABCD-A′B′C′D′中,
设O是AC′的中点,则$\overrightarrow{AO}$=$\frac{1}{2}\overrightarrow{A{C}^{'}}$=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{'})}$,
设P、M、N分别是BD′、CA′、DB′的中点,
则$\overrightarrow{AP}$=$\overrightarrow{AB}+\overrightarrow{BP}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{B{D}^{'}}$=$\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{B{B}^{'}})$
=$\overrightarrow{AB}+\frac{1}{2}(-\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{'}})$=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{'}})$,
同理,得:$\overrightarrow{AM}$=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{'}})$,
$\overrightarrow{AN}$=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{'}})$,
∴O、P、M、N四点重合,
∴对角线AC′、BD′、CA′、DB′交于一点,且在交点处互相平分.
点评 本题考查平行六面体的对角线交于一点,并且在交点处互相平分的证明,是中档题,解题时要认真审题,注意向量法的合理运用.

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案| A. | [-2,0] | B. | (-2,0) | C. | (-∞,-2) | D. | (-∞,-2)∪(0,+∞) |
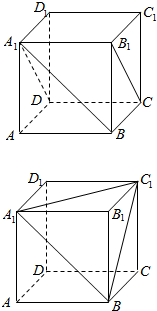 正方体ABCD-A1B1C1D1中.
正方体ABCD-A1B1C1D1中.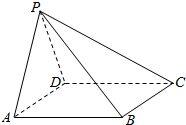 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是菱形,∠BAD=60°,PA=PD=AB=2.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是菱形,∠BAD=60°,PA=PD=AB=2. 如图,将一根长为m的铁丝弯曲围成一个上面是半圆,下方是矩形的形状.
如图,将一根长为m的铁丝弯曲围成一个上面是半圆,下方是矩形的形状.