题目内容
8.已知ω>0,在函数y=sinωx与y=cosωx的图象的交点中,相邻的三个交点恰好为一个等边三角形的三个顶点,则ω=$\frac{\sqrt{6}}{2}$π.分析 根据题意画出图形,结合图形求出函数y=sinωx与y=cosωx的图象交点中,线段AB、AC的大小,利用等边三角形边长相等列出方程,即可得出ω的值.
解答 解:如图所示,
ω>0,在函数y=sinωx与y=cosωx的图象交点中,
∴$\frac{T}{2}$=$\frac{π}{ω}$,
∴|AB|=$\sqrt{{(\frac{π}{ω})}^{2}{+(\sqrt{2})}^{2}}$,
|AC|=T=$\frac{2π}{ω}$;
又|AB|=|AC|,
即$\sqrt{{(\frac{π}{ω})}^{2}{+(\sqrt{2})}^{2}}$=$\frac{2π}{ω}$,
解得ω=$\frac{\sqrt{6}}{2}$π.
故答案为:$\frac{\sqrt{6}}{2}$π.
点评 本题主要考查了正弦、余弦函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知全集U=R,M={x|x≤1},P={x|x≥2},则∁U(M∪P)=( )
| A. | {x|1<x<2} | B. | {x|x≥1} | C. | {x|x≤2} | D. | {x|x≤1或x≥2} |
13.某游戏规则如下:随机地往半径为4的圆内投掷飞标,若飞镖到圆心的距离大于2,则成绩为及格;若飞镖到圆心的距离小于1,则成绩为优秀;若飞镖到圆心的距离大于或等于1且小于或等于2,则成绩为良好,那么在所有投掷到圆内的飞镖中得到成绩为良好的概率为( )
| A. | $\frac{1}{16}$ | B. | $\frac{3}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
11.已知三棱锥P-ABC,在底面△ABC中,∠A=60°,BC=$\sqrt{3}$,PA⊥面ABC,PA=2$\sqrt{3}$,则此三棱锥的外接球的表面积为( )
| A. | $\frac{16}{3}$π | B. | 4$\sqrt{3}$π | C. | $\frac{32}{3}$π | D. | 16π |
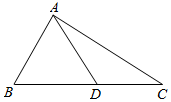 如图,在△ABC中,B=$\frac{π}{3}$,AC=$\sqrt{3}$,D为BC边上一点.若AB=AD,则△ADC的周长的取值范围为.
如图,在△ABC中,B=$\frac{π}{3}$,AC=$\sqrt{3}$,D为BC边上一点.若AB=AD,则△ADC的周长的取值范围为.