题目内容
16.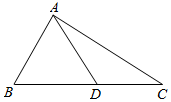 如图,在△ABC中,B=$\frac{π}{3}$,AC=$\sqrt{3}$,D为BC边上一点.若AB=AD,则△ADC的周长的取值范围为.
如图,在△ABC中,B=$\frac{π}{3}$,AC=$\sqrt{3}$,D为BC边上一点.若AB=AD,则△ADC的周长的取值范围为.
分析 由正弦定理可得AB=2sinC,BC=2sinA,由AD=AB,B=60°可知A>60°,结合图形可知周长l=AD+AC+DC=2sinA+$\sqrt{3}$,结合正弦函数的性质可求.
解答 解:∵AD=AB,B=60°,
∴A>60°.
∵B=$\frac{π}{3}$,AC=$\sqrt{3}$,
∴A+C=120°即A=120°-C
由正弦定理可得AB=2sinC,BC=2sinA
∴CD=2sinA-2sinC
周长l=AD+AC+DC=2sinA+$\sqrt{3}$,
∵60°<A<120°
∴$\frac{\sqrt{3}}{2}$<sinA≤1
∴2$\sqrt{3}$<l≤2+$\sqrt{3}$.
故答案为:2$\sqrt{3}$<l≤2+$\sqrt{3}$.
点评 本题主要考查了正弦定理在求解三角形中的应用,正弦函数的性质的灵活应用是求解本题的关键.

练习册系列答案
相关题目
6.若z=i(1+i),则|z|等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
4.某校高一年级开设了校本课程,现从甲、乙两班各随机抽取了5名学生校本课程的学分,统计如下表,s1,s2分别表示甲,乙两班抽取的5名学生学分的标准差,则( )
| 甲 | 8 | 11 | 14 | 15 | 22 |
| 乙 | 6 | 7 | 10 | 23 | 24 |
| A. | s1>s2 | B. | s1<s2 | ||
| C. | s1=s2 | D. | s1,s2大小不能确定 |