题目内容
已知空间四点A（2，-1，1），B（3，1，2），C（6，3，1），D（3，-2，2），试证明：AD⊥平面ABC；并求点D到平面ABC的距离．
考点：点、线、面间的距离计算,向量的数量积判断向量的共线与垂直
专题：圆锥曲线的定义、性质与方程
分析：求出
，
，
，利用向量的数量积为0，证明AD⊥平面ABC；利用向量的模点D到平面ABC的距离．
| AD |
| AB |
| AC |
解答：
解：空间四点A（2，-1，1），B（3，1，2），C（6，3，1），D（3，-2，2），
可得：
=（1，-1，1），
=（1，2，1），
=（4，4，0），
∵
•
=1-2+1=0，
•
=4-4+0=0，
∴
⊥
，
⊥
，并且
与
不共线，
∴AD⊥平面ABC；
点D到平面ABC的距离就是
|=
=
．
可得：
| AD |
| AB |
| AC |
∵
| AD |
| AB |
| AD |
| AC |
∴
| AD |
| AB |
| AD |
| AC |
| AB |
| AC |
∴AD⊥平面ABC；
点D到平面ABC的距离就是
| |AD |
| 12+(-1)2+12 |
| 3 |
点评：本题考查空间向量的数量积证明直线与平面垂直，点到平面的距离距离的求法，考查转化思想以及计算能力．
练习册系列答案
相关题目
方程ln（2x+1）=
的一个根落在区间（ ）（参考数值：ln1.5≈0.41，ln2≈0.69，ln2.5≈0.92）
| 1 |
| 3x+2 |
A、（-
| ||||
B、（0，
| ||||
C、（
| ||||
D、（
|
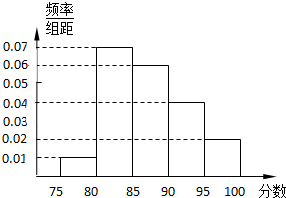某高中进行高中生歌唱比赛，在所有参赛成绩中随机抽取100名学生的成绩，按成绩分组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]得到的频率分布直方图如图所示．现在组委会决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试．定义在R上的函数f（x）=sinx+2xf′（
），f′（x）为f（x）的导函数，令a=-
，b=log32，则下列关系正确的是（ ）
| π |
| 3 |
| 1 |
| 2 |
| A、f（a）+f（b）＜0 |
| B、f（-a）+f（b）＞0 |
| C、f（a）+f（-b）＜0 |
| D、f（-a）+f（-b）＜0 |