题目内容
6．已知随机变量X+Y=10，若X～B（10，0.6），则E（Y），D（Y）分别是（ ）| A． | 6和2.4 | B． | 4和5.6 | C． | 4和2.4 | D． | 6和5.6 |
分析 先由X～B（10，0.6），得均值E（X）=6，方差D（X）=2.4，然后由X+Y=10得Y=-X+10，再根据公式求解即可．
解答 解：由题意X～B（10，0.6），知随机变量X服从二项分布，n=10，p=0.6，
则均值E（X）=np=6，方差D（X）=npq=2.4，
又∵X+Y=10，
∴Y=-X+10，
∴E（Y）=-E（X）+10=-6+10=4，
D（Y）=D（X）=2.4．
故选：C．
点评 解题关键是若两个随机变量Y，X满足一次关系式Y=aX+b（a，b为常数），当已知E（X）、D（X）时，则有E（Y）=aE（X）+b，D（Y）=a2D（X）．
练习册系列答案
相关题目
14．已知$cos（{α-\frac{π}{3}}）=-\frac{1}{2}$，则$sin（{\frac{π}{6}+α}）$的值等于（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | $-\frac{1}{2}$ |
11．2017年是某市大力推进居民生活垃圾分类的关键一年，有关部门为宣传垃圾分类知识，面向该市市民进行了一次“垃圾分类知识”的网络问卷调查，每位市民仅有一次参与机会，通过抽样，得到参与问卷调查中的1000人的得分数据，其频率分布直方图如图所示：
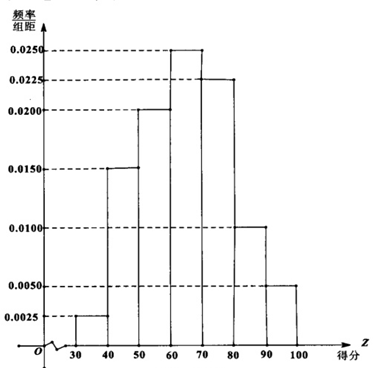
（1）由频率分布直方图可以认为，此次问卷调查的得分Z服从正态分布N（μ，210），μ近似为这1000人得分的平均值（同一组数据用该区间的中点值作代表），利用该正态分布，求P（50.5＜Z＜94）．
（2）在（1）的条件下，有关部门为此次参加问卷调查的市民制定如下奖励方案：
①得分不低于μ可获赠2次随机话费，得分低于μ则只有1次；
②每次赠送的随机话费和对应概率如下：
现有一位市民要参加此次问卷调查，记X（单位：元）为该市民参加问卷调查获赠的话费，求X的分布列．
附：$\sqrt{210}$≈14.5
若Z～N（μ，δ2），则P（μ-δ＜Z＜μ+δ）=0.6826，P（μ-2δ＜Z＜μ+2δ）=0.9544．
（1）由频率分布直方图可以认为，此次问卷调查的得分Z服从正态分布N（μ，210），μ近似为这1000人得分的平均值（同一组数据用该区间的中点值作代表），利用该正态分布，求P（50.5＜Z＜94）．
（2）在（1）的条件下，有关部门为此次参加问卷调查的市民制定如下奖励方案：
①得分不低于μ可获赠2次随机话费，得分低于μ则只有1次；
②每次赠送的随机话费和对应概率如下：
| 赠送话费（单位：元） | 10 | 20 |
| 概率 | $\frac{2}{3}$ | $\frac{1}{3}$ |
附：$\sqrt{210}$≈14.5
若Z～N（μ，δ2），则P（μ-δ＜Z＜μ+δ）=0.6826，P（μ-2δ＜Z＜μ+2δ）=0.9544．
如图，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的右顶点为A（2，0），左、右焦点分别为F1、F2，过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P，与椭圆交于另一个点B，且点B在x轴上的射影恰好为点F1．
15．命题“?x＞1，${（\frac{1}{2}）^x}＜\frac{1}{2}$”的否定是（ ）
| A． | ?x＞1，${（\frac{1}{2}）^x}≥\frac{1}{2}$ | B． | ?x≤1，${（\frac{1}{2}）^x}≥\frac{1}{2}$ | C． | ?x0＞1，${（\frac{1}{2}）^{x_0}}≥\frac{1}{2}$ | D． | ?x0≤1，${（\frac{1}{2}）^{x_0}}≥\frac{1}{2}$ |
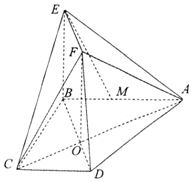如图所示，直角梯形ABCD两条对角线AC，BD的交点为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，M为线段AB上一点，AM=2MB，且AB⊥BC，AB∥CD，AB=BE=6，CD=BC=3．