题目内容
17.设f(x)=|x-b|+|x+b|.(1)当b=1时,求f(x)≤x+2的解集;
(2)当x=1时,若不等式f(x)≥$\frac{|a+1|-|2a-1|}{|a|}$对任意实数a≠0恒成立,求实数b的取值范围.
分析 (1)运用绝对值的含义,对x讨论,分x≥1,-1<x<1,x≤-1,去掉绝对值,得到不等式组,解出它们,再求并集即可得到解集;
(2)运用绝对值不等式的性质,可得不等式右边的最大值为3,再由不等式恒成立思想可得f(b)≥3,再由去绝对值的方法,即可解得b的范围.
解答 解:(1)当b=1时,f(x)=|x-1|+|x+1|,
由f(x)≤x+2得:
$\left\{\begin{array}{l}{x≥1}\\{x-1+x+1≤x+2}\end{array}\right.$或$\left\{\begin{array}{l}{-1<x<1}\\{1-x+x+1≤x+2}\end{array}\right.$或$\left\{\begin{array}{l}{x≤-1}\\{1-x-x-1≤x+2}\end{array}\right.$,
即有1≤x≤2或0≤x<1或x∈∅,
解得0≤x≤2,
所以f(x)≤x+2的解集为[0,2];
(2)$\frac{|a+1|-|2a-1|}{|a|}$=|1+$\frac{1}{a}$|-|2-$\frac{1}{a}$|≤|1+$\frac{1}{a}$+2-$\frac{1}{a}$|=3,
当且仅当(1+$\frac{1}{a}$)(2-$\frac{1}{a}$)≤0时,取等号.
由不等式f(x)≥$\frac{|a+1|-|2a-1|}{|a|}$对任意实数a≠0恒成立,
由于x=1,可得|1-b|+|1+b|≥3,
即$\left\{\begin{array}{l}{b≥1}\\{b-1+b+1≥3}\end{array}\right.$或$\left\{\begin{array}{l}{-1<b<1}\\{1-b+b+1≥3}\end{array}\right.$或$\left\{\begin{array}{l}{b≤-1}\\{1-b-b-1≥3}\end{array}\right.$,
解得:$b≤-\frac{3}{2}$或$b≥\frac{3}{2}$.
故实数b的取值范围是$(-∞,-\frac{3}{2}]∪[\frac{3}{2},+∞)$.
点评 本题考查绝对值不等式的解法,同时考查不等式恒成立问题的求法,运用分类讨论的思想方法和绝对值不等式的性质是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | {-1,2} | B. | {0,1} | C. | {-1,0} | D. | {0,2} |
| A. | 总能分别作出正弦线、余弦线、正切线 | |
| B. | 总能分别作出正弦线、余弦线、正切线,但可能不只一条 | |
| C. | 正弦线、余弦线、正切线都可能不存在 | |
| D. | 正弦线、余弦线总存在,但正切线不一定存在 |
| 古文迷 | 非古文迷 | 合计 | |
| 男生 | 26 | 24 | 50 |
| 女生 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
(Ⅱ)现从调查的女生中按分层抽样的方法抽出5人进行调查,求所抽取的5人中“古文迷”和“非古文迷”的人数;
(Ⅲ)现从(Ⅱ)中所抽取的5人中再随机抽取3人进行调查,记这3人中“古文迷”的人数为ξ,求随机变量ξ的分布列与数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
| A. | 6和2.4 | B. | 4和5.6 | C. | 4和2.4 | D. | 6和5.6 |
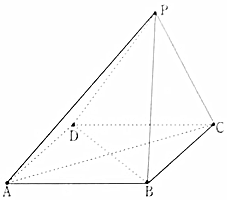 已知在四棱锥P-ABCD中,底面ABCD是平行四边形,且有PB=PD,PA⊥BD.
已知在四棱锥P-ABCD中,底面ABCD是平行四边形,且有PB=PD,PA⊥BD.