题目内容
在焦点分别为F1、F2的双曲线上有一点P，若∠F1PF2=
，|PF2|=2|PF1|，则该双曲线的离心率等于（ ）
| π |
| 3 |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
考点：双曲线的简单性质
专题：计算题,解三角形,圆锥曲线的定义、性质与方程
分析：由双曲线的定义，结合条件求出|PF2|=4a，|PF1|=2a，再由余弦定理，即可得到a，c的关系式，再由离心率公式，即可得到．
解答：
解：由于|PF2|=2|PF1|，
则P在双曲线的左支上，
则|PF2|-|PF1|=2a，
解得，|PF2|=4a，|PF1|=2a，
由于∠F1PF2=
，
则在△F1PF2中，由余弦定理，可得，
cos60°=
=
=
，
则有c=
a，即有e=
=
．
故选D．
则P在双曲线的左支上，
则|PF2|-|PF1|=2a，
解得，|PF2|=4a，|PF1|=2a，
由于∠F1PF2=
| π |
| 3 |
则在△F1PF2中，由余弦定理，可得，
cos60°=
| |PF1|2+|PF2|2-|F1F2|2 |
| 2|PF1|•|PF2| |
=
| 4a2+16a2-4c2 |
| 2•2a•4a |
| 1 |
| 2 |
则有c=
| 3 |
| c |
| a |
| 3 |
故选D．
点评：本题考查双曲线的定义和性质，考查余弦定理的运用，考查运算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知等差数列{an}的前n项和为Sn，S9=-18，S13=-52，{bn}为等比数列，且b5=a5，b7=a7，则b15的值为（ ）
| A、64 | B、128 |
| C、-64 | D、-128 |
在△ABC中，∠ABC=60°，AB=2，BC=6，在BC上任取一点D，使△ABD为钝角三角形的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示：给出函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤
）的图象的一段，则f（x）的表达式为（ ）
| π |
| 2 |
A、y=2sin（x+
| ||
B、y=2sin（x-
| ||
C、y=-2sin（2x+
| ||
D、y=2sin（2x+
|
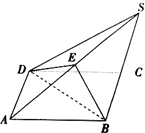如图所示，四边形ABCD是平行四边形，直线SC⊥平面ABCD，E是SA的中点，求证：平面BDE⊥平面ABCD．