题目内容
已知二次函数f(x)=x2+2x-1,若奇函数h(x)的定义域和值域都是区间(-k,k),且x∈(-k,0)时,h(x)=-f(x)-1,求k的值.
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:由题设条件,根据奇函数的性质求出h(x)在[-k,k]上的解析式,再根据其定义域和值域都是区间[-k,k],即可得到关于k的等式求出k的值.
解答:
解:由于f(x)=x2+2x-1,
且奇函数h(x)在x∈(-k,0)时,h(x)=-f(x)-1=-x2-2x,
则当x∈[0,k]时,h(x)=-h(-x)=x2-2x,
则有h(x)=
,
由x2-2x=x,可得x=3,
由-x2-2x=x,可得x=-3,
由图象可得x∈[-1,1]时,h(x)∈[-1,1]
当x∈[-3,3]时,h(x)∈[-3,3]
则有k=1或k=3.
且奇函数h(x)在x∈(-k,0)时,h(x)=-f(x)-1=-x2-2x,
则当x∈[0,k]时,h(x)=-h(-x)=x2-2x,
则有h(x)=
|
由x2-2x=x,可得x=3,
由-x2-2x=x,可得x=-3,
由图象可得x∈[-1,1]时,h(x)∈[-1,1]
当x∈[-3,3]时,h(x)∈[-3,3]
则有k=1或k=3.
点评:本题考查函数的奇偶性的运用,考查函数的解析式的求法,考查二次函数的值域问题,属于中档题和易错题.

练习册系列答案
相关题目
函数f(x)=
( )
| 3x-1 |
| 3x+1 |
| A、是偶函数,但不是奇函数 |
| B、是奇函数,但不是偶函数 |
| C、既是奇函数,又是偶函数 |
| D、不是奇函数,也不是偶函数 |
已知命题p:?a∈R,函数y=ax是单调函数,则¬p( )
| A、?a∈R,函数y=ax不一定是单调函数 |
| B、?a∈R,函数y=ax不是单调函数 |
| C、?a∈R,函数y=ax不一定是单调函数 |
| D、?a∈R,函数y=ax不是单调函数 |
对于定义域为R的函数f(x),若f(x)在(-∞,0)和(0,+∞)上均有零点,则称函数f(x)为“含界点函数”,则下列四个函数中,不是“含界点函数”的是( )
| A、f(x)=x2+bx-1(b∈R) |
| B、f(x)=2-|x-1| |
| C、f(x)=2x-x2 |
| D、f(x)=x-sinx |
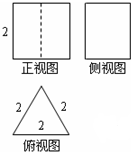 已知一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在一个球面上,则球的表面积是( )
已知一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在一个球面上,则球的表面积是( )A、
| ||
B、
| ||
C、
| ||
D、
|