题目内容
12．在△ABC中，a=1，c=$\sqrt{3}$，A=30°，则C=60°或120°．分析 由正弦定理可得sinC，结合三角形内角的范围和三角形的边角关系可得．
解答 解：∵在△ABC中，a=1，c=$\sqrt{3}$，A=30°，
∴由正弦定理可得sinC=$\frac{csinA}{a}$=$\frac{\sqrt{3}}{2}$，
∴C=60°或120°
故答案为：60°或120°
点评 本题考查正弦定理，属基础题．
练习册系列答案
相关题目
7．（cos75°+sin75°）2=（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
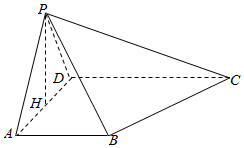如图所示，在四棱锥P-ABCD中，AB⊥平面PAD，AB∥CD且2AB=CD，PD=PA，点H为线段AD的中点，若$PH=1，AD=\sqrt{2}$，PB与平面ABCD所成角的大小为45°．