题目内容
3.已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=(-$\sqrt{3}$,x),且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为60°,则x=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据向量的夹角公式计算即可.
解答 解:∵向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=(-$\sqrt{3}$,x),
∴$\overrightarrow{a}•\overrightarrow{b}$=-$\sqrt{3}$+$\sqrt{3}$x,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=$\sqrt{3+{x}^{2}}$,
∵$\overrightarrow{a}$与$\overrightarrow{b}$夹角为60°,
∴cos60°=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{-\sqrt{3}+\sqrt{3}x}{2•\sqrt{3+{x}^{2}}}$=$\frac{1}{2}$,
∴x=3,
故选:C.
点评 本题考查了向量的数量积的运算以及向量的夹角,属于基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
8.若在曲线y=a2x+x+1(a>0,且a≠1)上的点(0,m)处的切线与直线mx-y+1=0平行,则m+a=( )
| A. | 1+e | B. | 1+$\sqrt{e}$ | C. | 2+e | D. | 2+$\sqrt{e}$ |
10.定义在实数集R上的偶函数y=f(x)满足f(x+1)=f(1-x),且在区间[-1,0]上单调递增,设a=f(1),$b=f({\sqrt{2}})$,c=f(2),则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | a>c>b |
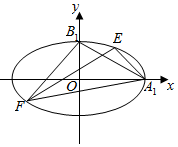 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,点E($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,设点A1,B1分别是椭圆的右顶点和上顶点,过点A1,B1引椭圆C的两条弦A1E、B1F.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,点E($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,设点A1,B1分别是椭圆的右顶点和上顶点,过点A1,B1引椭圆C的两条弦A1E、B1F.