题目内容
1.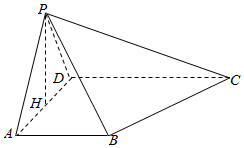 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD且2AB=CD,PD=PA,点H为线段AD的中点,若$PH=1,AD=\sqrt{2}$,PB与平面ABCD所成角的大小为45°.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD且2AB=CD,PD=PA,点H为线段AD的中点,若$PH=1,AD=\sqrt{2}$,PB与平面ABCD所成角的大小为45°.(1)证明:PH⊥平面ABCD;
(2)求四棱锥P-ABCD的体积.
分析 (1)由AB⊥平面PAD,可得平面PAD⊥平面ABCD,再由已知求得PH⊥AD,由面面垂直的性质得到PH⊥平面ABCD;
(2)由(1)可得∠PBH为PB与平面ABCD所成角等于45°,求解直角三角形BAH得到AB,进一步得到CD,求得底面直角梯形的面积,代入棱锥体积公式得答案.
解答 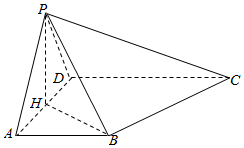 (1)证明:如图,∵AB⊥平面PAD,AB?平面ABCD,
(1)证明:如图,∵AB⊥平面PAD,AB?平面ABCD,
∴平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
又PD=PA,点H为线段AD的中点,
∴PH⊥AD,则PH⊥平面ABCD;
(2)解:在△PAD中,∵H为线段AD的中点,AD=$\sqrt{2}$,
∴AH=$\frac{\sqrt{2}}{2}$,
由(1)知,PH⊥平面ABCD,
连接BH,则∠PBH为PB与平面ABCD所成角等于45°,
在Rt△PHB中,由∠PBH=45°,得PH=BH=1,
在Rt△BAH中,有AB=$\sqrt{B{H}^{2}-A{H}^{2}}=\sqrt{1-(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{2}}{2}$,
则CD=2AB=$\sqrt{2}$,
∴${S}_{ABCD}=\frac{1}{2}×(\frac{\sqrt{2}}{2}+\sqrt{2})×\sqrt{2}=\frac{3}{2}$,
∴${V}_{P-ABCD}=\frac{1}{3}×{S}_{ABCD}×PH=\frac{1}{3}×\frac{3}{2}×1$=$\frac{1}{2}$.
点评 本题考查直线与平面垂直的判定,考查了面面垂直的性质,考查了棱锥体积的求法,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点F向其一条渐近线作垂线l,垂足为A,l与另一条渐近线交于B点,若$\overrightarrow{FB}$=3$\overrightarrow{FA}$,则双曲线的离心率为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | 2 | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$ |
13.在空间直角坐标系中,点B是点A(1,2,3)在坐标平面xOy上的射影,O为坐标原点,则OB的长为( )
| A. | $\sqrt{10}$ | B. | $\sqrt{13}$ | C. | $\sqrt{14}$ | D. | $\sqrt{5}$ |
10.定义在实数集R上的偶函数y=f(x)满足f(x+1)=f(1-x),且在区间[-1,0]上单调递增,设a=f(1),$b=f({\sqrt{2}})$,c=f(2),则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | a>c>b |