题目内容
4．若实数x，y满足约束条件$\left\{\begin{array}{l}y≥0\\ y≤x\\ y≤-2x+9\end{array}\right.$，则z=x+3y的最大值等于（ ）| A． | 0 | B． | $\frac{9}{2}$ | C． | 12 | D． | 27 |
分析 由约束条件作出可行域，数形结合得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案．
解答 解：由约束条件$\left\{\begin{array}{l}y≥0\\ y≤x\\ y≤-2x+9\end{array}\right.$，作出可行域如图，
联立$\left\{\begin{array}{l}{y=x}\\{y=-2x+9}\end{array}\right.$，解得：A（3，3），
化目标函数z=x+3y为y=-$\frac{1}{3}x$+$\frac{1}{3}z$，
由图可知，当直线y=-$\frac{1}{3}x$+$\frac{1}{3}z$过A时，直线在y轴上的截距最大，z最大．
此时z=3+3×3=12．
故选：C．
点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
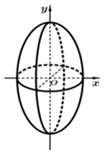祖暅（公元前5～6世纪）是我国齐梁时代的数学家，是祖冲之的儿子．他提出了一条原理：“幂势既同，则积不容异．”这里的“幂”指水平截面的面积，“势”指高．这句话的意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体体积相等．设由椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1（a＞b＞0）所围成的平面图形绕y轴旋转一周后，得一橄榄状的几何体（如图）（称为椭球体），课本中介绍了应用祖暅原理求球体体积公式的做法，请类比此法，求出椭球体体积，其体积等于$\frac{4}{3}π×{b^2}a$．
9．已知命题$p：?x∈（{0，+∞}），lnx≥2\frac{x-1}{x+1}$，则￢p为（ ）
| A． | $?{x_0}∈（{0，+∞}），lnx≥2\frac{x-1}{x+1}$ | B． | $?{x_0}∈（{0，+∞}），lnx＜2\frac{x-1}{x+1}$ | ||
| C． | $?x∈（{0，+∞}），lnx＜2\frac{x-1}{x+1}$ | D． | 不存在${x_0}∈（{0，+∞}），lnx＜2\frac{x-1}{x+1}$ |
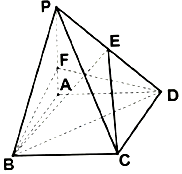如图，四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD为菱形，$2\overrightarrow{AF}=\overrightarrow{FP}$，$\overrightarrow{PE}=λ\overrightarrow{ED}$，∠ABC=60°，PA=3，AB=2．