题目内容
14.已知圆C:(x+1)2+y2=12及点F(1,0)点,P在圆上,M,N分别为PF、PC上的点,且满足$\overrightarrow{PM}$=$\overrightarrow{MF}$,$\overrightarrow{MN}$•$\overrightarrow{PF}$=0(1)求N的轨迹W的方程;
(2)是否存在过点F(1,0)的直线l与曲线W相交于A,B两点,并且与曲线W上一点Q,使得四边形OAQB为平行四边形?若存在,求出直线l的方程;若不存在,说明理由.
分析 (1)推导出曲线W是以C,F为焦点的椭圆,且a=$\sqrt{3}$,c=1,b=$\sqrt{2}$,由此能求出曲线C的方程.
(2)设l:x=my+1,代入椭圆方程整理得(2m2+3)y2+4my-4=0,由此利用根的判别式、韦达定理、向量知识、椭圆性质,结合已知条件能求出直线l的方程.
解答 (本小题满分13分)
解:(1)由M,N分别为PF、PC上的点,且满足$\overrightarrow{PM}$=$\overrightarrow{MF}$,$\overrightarrow{MN}$•$\overrightarrow{PF}$=0
得道直线MN为线段PF的中垂线,则|PN|=|NF|,
因此|NC|+|NF|=2$\sqrt{3}$,曲线W是以C,F为焦点的椭圆,且a=$\sqrt{3}$,c=1,b=$\sqrt{2}$,
所以曲线C的方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.…(6分)
(2)设A(x1,y1),B(x2,y2),由题意知l的斜率一定不为0,
故不妨设l:x=my+1,代入椭圆方程整理得(2m2+3)y2+4my-4=0,…(7分)
△=16m2+16(2m2+3)>0,
${y}_{1}+{y}_{2}=-\frac{4m}{2{m}^{2}+3}$,${y}_{1}{y}_{2}=-\frac{4}{2{m}^{2}+3}$,①,…(8分)
假设存在点Q,使得四边形OAQB为平行四边形,其充要条件为$\overrightarrow{OQ}=\overrightarrow{OA}+\overrightarrow{OB}$,
则点Q的坐标为(x1+x2,y1+y2).由点Q在椭圆上,即$\frac{({x}_{1}+{x}_{2})^{2}}{3}$+$\frac{({y}_{1}+{y}_{2})^{2}}{2}$=1,
整理得$2{{x}_{1}}^{2}+3{{y}_{1}}^{2}+2{{x}_{2}}^{2}+3{{y}_{2}}^{2}+4{x}_{1}{x}_{2}$+6y1y2=6,…(10分)
又A,B在椭圆上,即$2{{x}_{1}}^{2}+3{{y}_{1}}^{2}=6,2{{x}_{2}}^{2}+3{{y}_{2}}^{2}=6$,
故2x1x2+3y1y2=-3,②…(11分)
所以x1x2=(my1+1)(my2+1)=m2y1y2+m(y1+y2)+1,
将①②代入上式解得m=$±\frac{\sqrt{2}}{2}$,…(12分)
即直线l的方程是:x=$±\frac{\sqrt{2}}{2}$y+1,即2x$±\sqrt{2}y$-2=0.…(13分)
点评 本题考查曲线方程的求法,考查满足条件的直线方程是否存在的判断与求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、向量知识、椭圆性质的合理运用.

| A. | 0 | B. | $\frac{9}{2}$ | C. | 12 | D. | 27 |
| A. | (4,2,2,2) | B. | (9,0,1,0) | C. | (8,0,1,1) | D. | (7,0,1,2) |
| A. | (0,$\frac{1}{4}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | (1,2) |
| A. | 若p∨q是真命题,则p,q都是真命题 | |
| B. | 命题“?x0∈R,x02-1>0的否定是“?x∈R,x2-1<0” | |
| C. | 过平面α外的一点P的直线与平面α所成的角为θ,则这样的直线有无数条 | |
| D. | △ABC中,“A>B”是“sinA>sinB”的充要条件 |
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 |
| 答对率 | 70% | 60% | 50% | 40% | 30% | 10% |
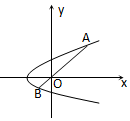 在抛物线y2=4a(x+a)(a>0),设有过原点O作一直线分别交抛物线于A、B两点,如图所示,试求|OA|•|OB|的最小值.
在抛物线y2=4a(x+a)(a>0),设有过原点O作一直线分别交抛物线于A、B两点,如图所示,试求|OA|•|OB|的最小值.