题目内容
15.已知函数$f(x)=\left\{{\begin{array}{l}{{x^2}+(4a-3)x+3a,x<0}\\{{{log}_a}(x+1)+1,x≥0}\end{array}}\right.(a>0且a≠1)$在R上单调递减,且关于x的方程$|f(x)|=2-\frac{x}{3}$恰有两个不相等的实数解,则a的取值范围是( )| A. | (0,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,$\frac{3}{4}$] | C. | [$\frac{1}{3}$,$\frac{2}{3}$] | D. | [$\frac{1}{3}$,$\frac{2}{3}$) |
分析 由减函数可知f(x)在两段上均为减函数,且在第一段的最小值大于或等于第二段上的最大值,作出|f(x)|和y=2-$\frac{x}{3}$的图象,根据交点个数判断3a与2的大小关系,列出不等式组解出.
解答 解: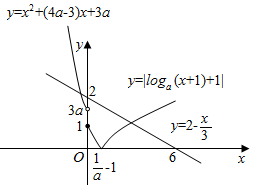 :∵f(x)是R上的单调递减函数,
:∵f(x)是R上的单调递减函数,
∴y=x2+(4a-3)x+3a在(-∞,0)上单调递减,y=loga(x+1)+1在(0,+∞)上单调递减,
且f(x)在(-∞,0)上的最小值大于或等于f(0).
∴$\left\{\begin{array}{l}{\frac{3-4a}{2}≥0}\\{0<a<1}\\{3a≥1}\end{array}\right.$,解得$\frac{1}{3}≤a≤\frac{3}{4}$.
作出y=|f(x)|和y=2-$\frac{x}{3}$的函数草图如图所示:
∵|f(x)|=2-$\frac{x}{3}$恰有两个不相等的实数解,
∴3a<2,即a<$\frac{2}{3}$.
综上,$\frac{1}{3}$≤a<$\frac{2}{3}$.
故选:D.
点评 本题考查了分段函数的单调性,函数零点的个数判断,结合函数函数图象判断端点值的大小是关键,属于中档题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
12.微信是腾讯公司推出的一种手机通讯软件,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户为“A组”,否则为“B组”,调查结果如下:
(1)根据以上数据,能否有60%的把握认为“A组”用户与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“A组”和“B组”的人数;
(3)从(2)中抽取的5人中再随机抽取2人赠送200元的护肤品套装,求这2人中至少有1人在“A组”的概率.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
| A组 | B组 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“A组”和“B组”的人数;
(3)从(2)中抽取的5人中再随机抽取2人赠送200元的护肤品套装,求这2人中至少有1人在“A组”的概率.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
10.设f(x)是定义在R上的函数,其导函数为f′(x),若f(x)+f′(x)>1,f(0)=2017,则不等式exf(x)>ex+2016(其中e为自然对数的底数)的解集为( )
| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (2016,+∞) | D. | (-∞,0)∪(2016,+∞) |
7.已知一个几何体的三视图如图所示,则该几何体的体积是( )
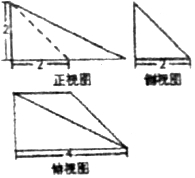

| A. | 2 | B. | 4 | C. | 6 | D. | 1 |
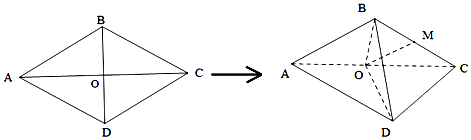
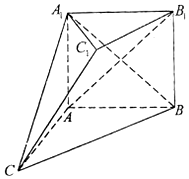 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC