题目内容
在△ABC中,sin2 A≤sin2 B+sin2 C-sin Bsin C,则A的取值范围是( ).
A. B.
B. C.
C. D.
D.
C
解析 由已知及正弦定理有a2≤b2+c2-bc,而由余弦定理可知a2=b2+c2-2bccos A,于是可得b2+c2-2bccos A≤b2+c2-bc,可得cos A≥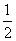 ,注意到在△ABC中,0<A<π,故A∈
,注意到在△ABC中,0<A<π,故A∈ .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 的图象上的两个相邻的最高点和最低点的距离为2
的图象上的两个相邻的最高点和最低点的距离为2 ,则ω=________.
,则ω=________. =3,则sin 2θ-2cos2θ的值为________.
=3,则sin 2θ-2cos2θ的值为________.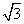 ,BC=
,BC= ,那么A等于( ).
,那么A等于( ). 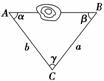
 +
+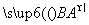 =2
=2 ,则( ).
,则( ). +
+ =0 B.
=0 B. +
+ ,平面内一点M满足
,平面内一点M满足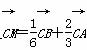 ,则
,则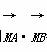 =________.
=________.