题目内容
已知x、y∈(0,2π)且满足
(cosx-sinx)=3sin2y-6siny+5,求x-y.
| 2 |
考点:三角函数的化简求值
专题:三角函数的求值,三角函数的图像与性质
分析:化简已知可得:3(siny-1)2+2=2cos(x+
),即有
,从而可求得x-y的值.
| π |
| 4 |
|
解答:
解:由题意可得:3sin2y-6siny+5=3(siny-1)2+2=
(cosx-sinx)=2cos(x+
),
∴3(siny-1)2+2=2cos(x+
),
∴上等式成立,有
,
∵x、y∈(0,2π),
∴可解得:y=
,x=π-
=
,
∴x-y=
-
=
.
| 2 |
| π |
| 4 |
∴3(siny-1)2+2=2cos(x+
| π |
| 4 |
∴上等式成立,有
|
∵x、y∈(0,2π),
∴可解得:y=
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
∴x-y=
| 3π |
| 4 |
| π |
| 2 |
| π |
| 4 |
点评:本题主要考察了三角函数的化简求值,三角函数值域的求法,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知两直线l1:2x-y+3=0,l2:mx+2y+n=0平行,则m的值是( )
| A、-4 | B、-1 | C、1 | D、4 |
已知圆柱的侧面展开图是边长分别为2a,a的矩形,则该圆柱的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
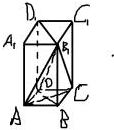 如图,在直棱柱ABCD-A1B1C1D1中,AA1=4,底面是边长为2的菱形,且∠BAD=60°.
如图,在直棱柱ABCD-A1B1C1D1中,AA1=4,底面是边长为2的菱形,且∠BAD=60°.