题目内容
已知函数f(x)=
,若存在k使得函数f(x)的值域是[0,2],则实数a的取值范围是 .
|
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用
分析:分别作出函数y=log2(1-x)+1,(x>-1)和y=x2-3x+2的图象,观察函数值在[0,2]内的图象,讨论最小值和最大值的情况,对a讨论,a=1,a>1,a<1,以及a<
,a≥
,的情况,即可得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
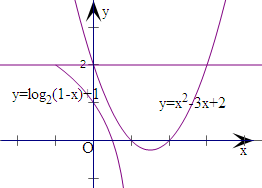 解:分别作出函数y=log2(1-x)+1,(x>-1)
解:分别作出函数y=log2(1-x)+1,(x>-1)
和y=x2-3x+2的图象,
由于函数f(x)的值域是[0,2],则观察函数值在[0,2]内的图象,
由于f(-1)=log22+1=2,f(0)=02-3×0+2=2,
显然a=0不成立,a=1成立,a>1不成立,
又f(
)=log2(1-
)+1=0,若a<
,则最小值0取不到,
则a≥
,
综上可得,
≤a≤1.
即有实数a的取值范围是[
,1].
故答案为:[
,1].
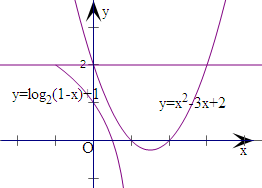 解:分别作出函数y=log2(1-x)+1,(x>-1)
解:分别作出函数y=log2(1-x)+1,(x>-1)和y=x2-3x+2的图象,
由于函数f(x)的值域是[0,2],则观察函数值在[0,2]内的图象,
由于f(-1)=log22+1=2,f(0)=02-3×0+2=2,
显然a=0不成立,a=1成立,a>1不成立,
又f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则a≥
| 1 |
| 2 |
综上可得,
| 1 |
| 2 |
即有实数a的取值范围是[
| 1 |
| 2 |
故答案为:[
| 1 |
| 2 |
点评:本题考查已知函数的值域,求参数的范围,考查数形结合的思想方法,注意观察和分析,考查运算能力,属于中档题和易错题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
函数f(x)=ln|x|-
x2的图象大致是( )
| 1 |
| 2 |
A、 |
B、 |
C、 |
D、 |