题目内容
13.记不等式x2+x-6<0的解集为集合A,函数y=lg(x-a)的定义域为集合B.(1)当a=-1时,求A∩B;
(2)若“x∈A”是“x∈B”的充分条件,求实数a的取值范围.
分析 (1)根据条件求出A,B,将a=-1代入,求出A∩B即可;(2)结合充分条件和必要条件的定义进行求解即可.
解答 解:由x2+x-6<0得-3<x<2,即A(-3,2),
由x-a>0,得x>a,即B=(a,+∞),
(1)若a=-1,则B=(-1,+∞),
故A∩B=(1,2);
(2)若“x∈A”是“x∈B”的充分条件,
则A⊆B,
即a≤-3.
点评 本题主要考查充分条件和必要条件的关系的应用,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线;
如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线MN与AC所成的角为60°.
则其中真命题的是( )
 如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线;
如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线; ②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线MN与AC所成的角为60°.
则其中真命题的是( )
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
1.已知定义在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{log_2}(x+1),{\;}_{\;}x∈[0,1]\\|x-3|-1,{\;}_{\;}x∈(1,+∞)\end{array}$,则关于x的方程f(x)=a,(0<a<1)的所有根之和为( )
| A. | 2a-1 | B. | 2a+1 | C. | 1-2-a | D. | 1+2-a |
3.已知极坐标的极点在直角坐标系的原点O处,极轴与x轴的正半轴重合.曲线C的参数方程为$\left\{\begin{array}{l}{x=3cosφ}\\{y=2sinφ}\end{array}\right.$(φ为参数),直线l的极坐标方程是ρ(cosθ+2sinθ)=15.若点P、Q分别是曲线C和直线l上的动点,则P、Q两点之间距离的最小值是( )
| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | $\sqrt{21}$ |
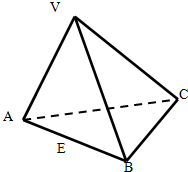 三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1,E为AB边中点.
三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1,E为AB边中点.