题目内容
12.在含有2件次品的10件产品中,任取3件,求:(1)取到的次品数X的分布列及数学期望;
(2)至少取到1件次品的概率.
分析 (1)由已知得X的可能取值为0,1,2分别求出相应的概率,由此能求出X的分布列.(2)利用对立事件的概率公式能求出至少取到1件次品的概率.
解答 解:(1)由已知得X的可能取值为0,1,2,
P(X=0)=$\frac{{C}_{8}^{3}}{{C}_{10}^{3}}$=$\frac{7}{15}$,
P(X=1)=$\frac{{{C}_{8}^{2}C}_{2}^{1}}{{C}_{10}^{3}}$=$\frac{7}{15}$,
P(X=2)=$\frac{{{C}_{8}^{1}C}_{2}^{2}}{{C}_{10}^{3}}$=$\frac{1}{15}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{7}{15}$ | $\frac{7}{15}$ | $\frac{1}{15}$ |
P=1-P(X=0)=1-$\frac{7}{15}$=$\frac{8}{15}$.
点评 本题考查概率的求法,考查离散型随机变量的分布列的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
11.已知$a={2^{\frac{6}{5}}},b={({\frac{1}{8}})^{-\frac{4}{5}}},c=2{log_5}2$,则a,b,c的大小关系为( )
| A. | c<b<a | B. | c<a<b | C. | b<a<c | D. | b<c<a |
12. 如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线;
如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线MN与AC所成的角为60°.
则其中真命题的是( )
 如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线;
如图所示,正方体 ABCD-A1B1C1D1中,M.N分别为棱 C1D1,C1C的中点,有以下四个结论:①直线AM与C1C是相交直线; ②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线MN与AC所成的角为60°.
则其中真命题的是( )
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
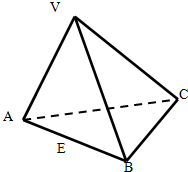 三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1,E为AB边中点.
三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1,E为AB边中点.