题目内容
11.已知实数x,y满足不等式组$\left\{\begin{array}{l}{1≤x+y≤2}\\{-1≤x-y≤1}\end{array}\right.$,则z=$\frac{y+1}{x+1}$的最大值是2.分析 作出不等式组对应平面区域,利用z的几何意义即可得到结论.
解答  解:作出不等式组对应的平面区域如图
解:作出不等式组对应的平面区域如图
则z=$\frac{y+1}{x+1}$的几何意义为动点P到定点Q(-1,-1)的斜率,
由图象可知当P位于A(0,1)时,直线AQ的斜率最大,
此时z=$\frac{1+1}{0+1}$=2,
故答案为:2.
点评 本题主要考查线性规划的应用,利用z的几何意义,以及直线的斜率公式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若回归直线的斜率$\widehatb∈(0,+∞)$,则相关系数r的取值范围为( )
| A. | (0,1] | B. | [-1,0) | C. | 0 | D. | 无法确定 |
16.已知函数f(x)=x3+ax2+bx有两个极值点x1、x2,且x1<x2,若x1+2x0=3x2,函数g(x)=f(x)-f(x0),则g(x)( )
| A. | 恰有一个零点 | B. | 恰有两个零点 | C. | 恰有三个零点 | D. | 至多两个零点 |
3.已知f(x)=ln(e2x+1)+xcos2x,则f($\frac{π}{3}$)-f(-$\frac{π}{3}$)=( )
| A. | 0 | B. | $\frac{π}{3}$ | C. | π | D. | $\frac{4π}{3}$ |
20.已知函数f(x)=x(m+e-x),其中e为自然对数的底数,曲线y=f(x)上存在不同的两点,使得曲线在这两点处的切线都与y轴垂直,则实数m的取值范围是( )
| A. | (0,e-2) | B. | (e-2,+∞) | C. | (0,e2) | D. | (e2,+∞) |
1.设A,B是非空集合,定义A*B={x|x∈A∪B且x∉A∩B},已知M={x|0≤x≤3},N={y|y≤1},则M*N=( )
| A. | (1,3] | B. | (-∞,0)∪(1,3] | C. | (-∞,3] | D. | (-∞,0]∪[1,3] |
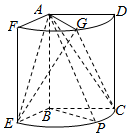 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.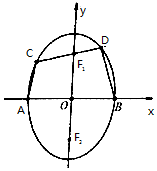 已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.
已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.