题目内容
从一批苹果中,随机抽取50个,其重量(单位:克)的频率分布如下.
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[85,90)和[95,100)的苹果中共抽取10个,其中重量在[95,100)的有几个?
(3)在(2)中抽取出的10个苹果中,任取3个,求重量不在同一个范围内的概率.
| 分组(重量) | [80,85﹚ | [85,90﹚ | [90,95﹚ | [95,100﹚ |
| 频数(个) | 5 | 15 | 20 | 10 |
(2)用分层抽样的方法从重量在[85,90)和[95,100)的苹果中共抽取10个,其中重量在[95,100)的有几个?
(3)在(2)中抽取出的10个苹果中,任取3个,求重量不在同一个范围内的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布表
专题:概率与统计
分析:(1)用苹果的重量在[90,95)的频数除以样本容量,即为所求.
(2)根据重量在[95,100)的频数所占的比例,求得重量在[95,100)的苹果的个数.
(3)用排列组合求出所有的基本事件的个数,再求出满足条件的事件的个数,即可得到所求事件的概率.
(2)根据重量在[95,100)的频数所占的比例,求得重量在[95,100)的苹果的个数.
(3)用排列组合求出所有的基本事件的个数,再求出满足条件的事件的个数,即可得到所求事件的概率.
解答:
解:(1)苹果的重量在[90,95)的频率为
=
=0.4.
(2)重量在[95,100)的有x个,则
=
,解得x=4个
(3)这10个苹果中,重量在[85,90)段的有6个,重量在[95,100)的有4个,
任取3个共有
=120种,重量在同一个范围的有
+
=24种,
则重量不在同一个范围内120-24=96
故重量不在同一个范围内的概率P=
=
| 20 |
| 50 |
| 2 |
| 5 |
(2)重量在[95,100)的有x个,则
| 10 |
| 15+10 |
| x |
| 10 |
(3)这10个苹果中,重量在[85,90)段的有6个,重量在[95,100)的有4个,
任取3个共有
| C | 3 10 |
| C | 3 6 |
| C | 3 4 |
则重量不在同一个范围内120-24=96
故重量不在同一个范围内的概率P=
| 96 |
| 120 |
| 4 |
| 5 |
点评:本题考查古典概型问题,还考查分层抽样的定义和方法,利用了总体中各层的个体数之比等于样本中对应各层的样本数之比,属于基础题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
直线l过圆x2+y2-2x+4y-4=0的圆心,且在y轴上的截距等于圆的半径,则直线l的方程为( )
| A、5x+y-3=0 |
| B、5x-y-3=0 |
| C、4x+y-3=0 |
| D、3x+2y-6=0 |
一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的体积为( ) 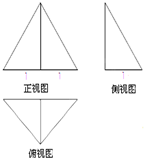

| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
若a>b,则下列不等式正确的是( )
| A、a-3>b-2 | ||||
| B、a+2>b+1 | ||||
| C、ac>bc | ||||
D、
|
函数f(x)=lnx+
x-2的零点所在区间为( )
| 1 |
| 2 |
| A、(0,1) |
| B、(2,3) |
| C、(1,2) |
| D、(3,4) |
若θ∈(0,
),则点P(θ-sinθ,θ-tanθ)在( )
| π |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 在“2013唱响资阳”电视歌手大赛中,七位评委给甲、乙两名选手打出的分数的茎叶图如右图所示,则甲、乙两名选手得分的中位数之和为
在“2013唱响资阳”电视歌手大赛中,七位评委给甲、乙两名选手打出的分数的茎叶图如右图所示,则甲、乙两名选手得分的中位数之和为