题目内容
点M、N分别是△OAB的边OA、OB上的点，
=
，
=
，
（1）若M、N分别是OA、OB的中点，线段AN与BM的交点为P，试用
，
表示
；
（2）若|
|：|
|=1：4，|
|：|
|=1：5，线段AN与BM交于点Q，试用
，
表示
．
| OA |
| a |
| OB |
| b |
（1）若M、N分别是OA、OB的中点，线段AN与BM的交点为P，试用
| a |
| b |
| OP |
（2）若|
| OM |
| OA |
| ON |
| OB |
| a |
| b |
| OQ |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：（1）利用重心的性质即可得出；
（2）利用向量共线定理和共面向量定理即可得出．
（2）利用向量共线定理和共面向量定理即可得出．
解答：
解：（1）由题意知，P为△OAB的重心，则
=
+
；
（2）设
=x
+y
，
依题
=4x
+y
，又B、M、Q三点共线，∴4x+y=1…①
同理
=x
+5y
，又A、N、Q三点共线，∴x+5y=1…②
由①、②解得x=
，y=
，
所以
=
+
．
| OP |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
（2）设
| OQ |
| a |
| b |
依题
| OQ |
| OM |
| OB |
同理
| OQ |
| OA |
| ON |
由①、②解得x=
| 4 |
| 19 |
| 3 |
| 19 |
所以
| OQ |
| 4 |
| 19 |
| a |
| 3 |
| 19 |
| b |
点评：本题考查了三角形的重心的性质、向量共线定理和共面向量定理，考查了推理能力和计算能力，属于中档题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
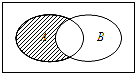已知全集U=R，集合A={0，1，2}，B={2，3，4}，如图阴影部分所表示的集合为（ ）| A、{2} |
| B、{0，1} |
| C、{3，4} |
| D、{0，1，2，3，4} |