题目内容
二项式（2x-
）6的展开式中的常数项是（ ）
| 1 |
| x |
| A、20 | B、-20 |
| C、160 | D、-160 |
考点：二项式系数的性质
专题：二项式定理
分析：先求出二项式展开式的通项公式，再令x的幂指数等于0，求得r的值，即可求得展开式中的常数项的值．
解答：
解：二项式（2x-
）6的展开式的通项公式为Tr+1=
•（-1）r•26-r•x6-2r，
令6-2r=0，求得r=3，可得展开式中的常数项是-8•
=-160，
故选：D．
| 1 |
| x |
| C | r 6 |
令6-2r=0，求得r=3，可得展开式中的常数项是-8•
| C | 3 6 |
故选：D．
点评：本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于基础题．
练习册系列答案
相关题目
某地西红柿自2月1日开始分批上市，通过市场调查，某批西红柿上市距2月1日的天数t与其种植成本Q（单位：元/100kg）的相关数据如表：
根据表中数据，下列函数模型中可以描述西红柿的种植成本Q与t的变化关系的是（ ）
| 时间t | 50 | 110 | 250 |
| 种植成本Q | 150 | 108 | 150 |
| A、Q=at+b（a≠0） |
| B、Q=at2+bt+c（a≠00 |
| C、Q=a•bt（a≠0） |
| D、Q=a•logbt（a≠0） |
若两直线3x+2y+m=0和x-4y+n=0的交点坐标为（-1，2），则m+n等于（ ）
| A、8 | B、10 | C、-8 | D、-10 |
已知集合{x|x2+（k+2）x+1=0，x∈R}∩R+=∅，则实数k的取值范围是（ ）
| A、-4＜k＜0 | B、k＞-4 |
| C、k＞-2 | D、k≥0 |
一个袋中装有大小相同的5个球，其中黑球2个和白球3个，现从袋中随机取出2个球，取出的两个球均为白球的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
的定义域是（ ）
| log2(1-x) | ||||
|
| A、（-∞，-1） |
| B、[-1，1] |
| C、（-1，1） |
| D、（1，+∞） |
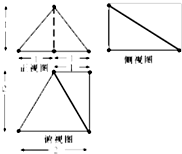
如图是某几何体的三视图，则该几何体的表面积为（ ）
A、
| ||||||||
B、
| ||||||||
C、4+
| ||||||||
D、
|
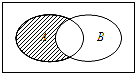已知全集U=R，集合A={0，1，2}，B={2，3，4}，如图阴影部分所表示的集合为（ ）| A、{2} |
| B、{0，1} |
| C、{3，4} |
| D、{0，1，2，3，4} |