题目内容

11．不等式$\frac{2}{x}＞-3$的解集是$（-∞，-\frac{2}{3}）$∪（0，+∞）．

分析 转化为求$\left\{\begin{array}{l}{x＞0}\\{2+3x＞0}\end{array}\right.$或$\left\{\begin{array}{l}{x＜0}\\{2+3x＜0}\end{array}\right.$的解集即可．

解答 解：∵$\frac{2}{x}＞-3$，
∴$\frac{2+3x}{x}＞0$，
∴$\left\{\begin{array}{l}{x＞0}\\{2+3x＞0}\end{array}\right.$或$\left\{\begin{array}{l}{x＜0}\\{2+3x＜0}\end{array}\right.$，
∴解得解集是：$（-∞，-\frac{2}{3}）$∪（0，+∞）．
故答案为：$（-∞，-\frac{2}{3}）$∪（0，+∞）．

点评 本题考查的是解一元一次不等式，熟知不等式的基本性质是解答此题的关键．

练习册系列答案
相关题目
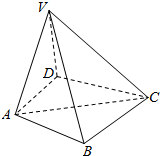1．已知sin（π+θ）=$\frac{1}{2}$，求$\frac{cos（3π+θ）}{cos[cos（π-θ）-1]}$+$\frac{cos（θ-2π）}{sin（θ-\frac{7π}{2}）cos（π-θ）-sin（\frac{3π}{2}+θ）}$的值．
2．如图，四棱锥V-ABCD中，∠BCD=∠BAD=90°，又∠BCV=∠BAV=90°求证：平面VDB⊥平面ABCD．
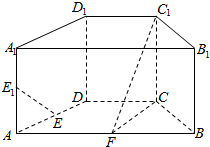19．如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，E、E1、F分别是棱AD、AA1、AB的中点．
（1）判断平面ADD1A1与平面FCC1的位置关系，并证明；
（2）证明：直线EE1∥平面FCC1．
6．已知函数f（x）=alnx+blgx+2，且$f（{\frac{1}{2009}}）=4$，则f（2009）的值为0．
16．已知 a、b、c分别为ABC三个内角A、B、C的对边，且ccosA-$\sqrt{3}$asinC-c=0
（1）求角A
（2）若a=2，△ABC的面积为$\sqrt{3}$，求b、c．
3．下面的数组均由三个数组成，它们是：（1，2，3），（2，4，6），（3，8，11），（4，16，20），（5，32，37），…，（an，bn，cn）．
（1）请写出数列{an}，{bn}，{cn}的通项公式，（无需证明）
（2）若数列{cn}的前n项和为Mn，求M10．
20．下列命题中，正确的有（　　）
①如果一条直线垂直于平面内的两条直线，那么这条直线和这个平面垂直．
②过直线l外一点P，有且仅有一个平面与l垂直．
③如果三条共点直线两两垂直，那么其中一条直线垂直于另两条直线确定的平面．
④垂直于角的两边的直线必垂直角所在的平面．
⑤过点A垂直于直线a的所有直线都在过点A垂直于a的平面内．
A．2个B．3个C．4个D．5个
1．若0＜x1＜x2＜1，则下列判断正确的有③．
①e${\;}^{{x}_{2}}$-e${\;}^{{x}_{1}}$＞lnx2-lnx1；②e${\;}^{{x}_{2}}$-e${\;}^{{x}_{1}}$＜lnx2-lnx1；③x2e${\;}^{{x}_{1}}$＞x1e${\;}^{{x}_{2}}$；④x2e${\;}^{{x}_{1}}$＜x1e${\;}^{{x}_{2}}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网