题目内容
15.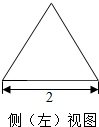 已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,那么此三棱柱正(主)视图的面积为$2\sqrt{3}$.表面积为$2\sqrt{3}$+12.体积为$2\sqrt{3}$.
已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,那么此三棱柱正(主)视图的面积为$2\sqrt{3}$.表面积为$2\sqrt{3}$+12.体积为$2\sqrt{3}$.
分析 由已知可得正三棱柱的所有棱长均为2,进而可得三视图中正视图的面积,及棱柱的表面积和体积.
解答 解:由已知可得正三棱柱的所有棱长均为2,
则此三棱柱的正视图为矩形,长2,宽$\sqrt{3}$,面积$2\sqrt{3}$,
表面积为:2×$\frac{\sqrt{3}}{4}×{2}^{2}$+6×2=$2\sqrt{3}$+12,
体积为:$\frac{\sqrt{3}}{4}×{2}^{2}$×2=$2\sqrt{3}$,
故答案为:$2\sqrt{3}$,$2\sqrt{3}$,$2\sqrt{3}$
点评 本题考查的知识点是棱柱的结构特征,由三视图求几何体的体积和表面积,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.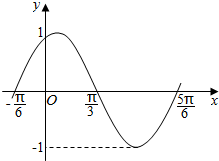 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )| A. | 向左平移$\frac{π}{6}$个长度单位,再把所得各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| B. | 向左平移$\frac{π}{3}$个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 | |
| C. | 向左平移$\frac{π}{3}$个长度单位,再把所得各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| D. | 向左平移$\frac{π}{6}$个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 |
10.若x,y∈R,则“x2>y2”是“x>y”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.用斜二测画法作出一个三角形的直观图,则原三角形面积是直观图面积的( )
| A. | $\frac{1}{2}$倍 | B. | 2$\sqrt{2}$倍 | C. | 2倍 | D. | $\frac{\sqrt{2}}{4}$倍 |
4.函数f(x)=x+$\frac{1}{x}$(x>0)的最小值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
5.在△ABC中,已知b2+c2-a2+bc=0,则角A等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
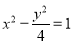 的右焦点为
的右焦点为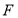 ,过点
,过点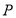 ,
,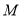 在直线
在直线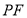 上, 且满足
上, 且满足 ,则
,则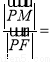 .
.