题目内容
20.已知数列{an}的前n项和为Sn,a1=2,且满足3Sn+4an-1=5an+3Sn-1(n≥2).(1)求数列{an}的通项公式;
(2)设bn=$\frac{{a}_{n}}{{(a}_{n}+1){(a}_{n+1}+1)}$,求数列{bn}的前n项和Tn.
分析 (1)利用an=Sn-Sn-1化简可知an=2an-1(n≥2),进而可知数列{an}是首项、公比均为2的等比数列,计算即得结论;
(2)通过(1)裂项可知bn=$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$,进而并项相加即得结论.
解答 解:(1)∵3Sn+4an-1=5an+3Sn-1(n≥2),
∴3an+4an-1=5an,即an=2an-1(n≥2),
又∵a1=2,
∴数列{an}是首项、公比均为2的等比数列,
于是其通项公式an=2n;
(2)由(1)可知bn=$\frac{{a}_{n}}{{(a}_{n}+1){(a}_{n+1}+1)}$=$\frac{{2}^{n}}{({2}^{n}+1)({2}^{n+1}+1)}$=$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$,
则Tn=$\frac{1}{2+1}$-$\frac{1}{{2}^{2}+1}$+$\frac{1}{{2}^{2}+1}$-$\frac{1}{{2}^{3}+1}$+…+$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$=$\frac{1}{3}$-$\frac{1}{{2}^{n+1}+1}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
13.已知a,b∈R,则“ab≥2”是“a2+b2≥4”成立的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
11.已知曲线f(x)=ke-x在点x=0处的切线与直线x-2y-1=0垂直,若x1,x2是函数g(x)=f(x)-|lnx|的两个零点,则( )
| A. | $\frac{1}{{e}^{2}}$<x1x2<$\frac{1}{e}$ | B. | $\frac{1}{{e}^{2}}$<x1x2<1 | C. | $\frac{1}{e}$<x1x2<1 | D. | e<x1x2<e2 |
8.已知一组数据x1,x2,…,xn的方差为2,若数据ax1+b,ax2+b,…,axn+b(a>0)的方差为8,则a的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
5.设x∈(0,$\frac{π}{2}$),若$\frac{1}{sinx}$+$\frac{1}{cosx}$=2$\sqrt{2}$,则sin(2x+$\frac{π}{3}$)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
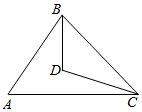 如图,D为△ABC内一点,并且满足AB=CD=4,∠A+∠BDC=180°,试确定S△ABC-S△BDC的最大值.
如图,D为△ABC内一点,并且满足AB=CD=4,∠A+∠BDC=180°,试确定S△ABC-S△BDC的最大值.