题目内容
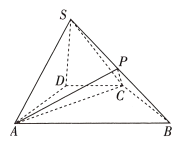
【题目】如图,正△ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
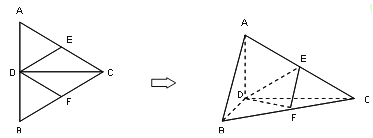
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求棱锥E-DFC的体积;
(3)在线段BC上是否存在一点P,使AP⊥DE?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1)![]() 平面
平面![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
本题主要考查线面垂直、线面平行、线线垂直、线线平行以及锥体体积问题,考查空间想象能力、运算能力和推理论证能力.第一问,在![]() 中,利用中位线得到
中,利用中位线得到![]() 与
与![]() 平行,通过线面平行的判断定理即可得到
平行,通过线面平行的判断定理即可得到![]() 平面
平面![]() ;第二问,要求三棱锥的体积,找到底面积和高是关键,通过
;第二问,要求三棱锥的体积,找到底面积和高是关键,通过![]() 的翻折得出
的翻折得出![]() 平面
平面![]() ,通过
,通过![]() ,得出
,得出![]() 平面
平面![]() ,所以
,所以![]() 为锥体的高,利用锥体体积公式计算出体积;第三问,在线段
为锥体的高,利用锥体体积公式计算出体积;第三问,在线段![]() 上取点
上取点![]() .使
.使![]() , 过
, 过![]() 作
作![]() 于
于![]() ,在
,在![]() 中,利用边长求出
中,利用边长求出![]() 的正切,从而确定角的度数,在等边三角形
的正切,从而确定角的度数,在等边三角形![]() 中,
中,![]() 是角平分线,所以
是角平分线,所以![]() ,再利用线面垂直的判定证出
,再利用线面垂直的判定证出![]() 平面
平面![]() ,所以
,所以![]() .
.
(1)![]() 平面
平面![]() ,理由如下:
,理由如下:
如图:在![]() 中,由
中,由![]() 分别是
分别是![]() 、
、![]() 中点,得
中点,得![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() .∴
.∴![]() 平面
平面![]() .
.
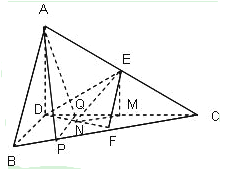
(2)∵![]() ,
,![]() ,将
,将![]() 沿
沿![]() 翻折成直二面角
翻折成直二面角![]() .
.
∴![]() ∴
∴![]() 平面
平面![]()
取![]() 的中点
的中点![]() ,这时
,这时![]() ∴
∴![]() 平面
平面![]() ,
,![]() ,
,
![]()
(3)在线段![]() 上存在点
上存在点![]() ,使
,使![]()
证明如下:在线段![]() 上取点
上取点![]() .使
.使![]() , 过
, 过![]() 作
作![]() 于
于![]() ,
,
∵![]() 平面
平面![]() ∴
∴![]() 平面
平面![]()
∴![]() , ∴
, ∴![]()
∴![]() ,又在等边
,又在等边![]() 中,
中,![]() ∴
∴![]()
∵![]() 平面
平面![]() ∴
∴![]() .
.![]()
∴![]() 平面
平面![]() , ∴
, ∴![]() .
.
此时![]() , ∴
, ∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目