Question

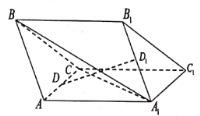
【题目】如图，在四棱锥中，底面为等腰梯形，，其中点在以为直径的圆上，，，，平面平面.

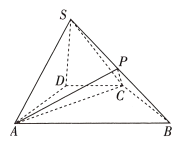
（1）证明：平面.

（2）设点是线段（不含端点）上一动点，当三棱锥的体积为1时，求异面直线与所成角的余弦值.

Answer 1

【答案】（1）详见解析；（2）.

【解析】

（1）利用余弦定理，由勾股定理可得，再根据面面垂直的性质可得平面；（2）设，则，由，解得，即点是线段的中点. 取的中点为，连接，可证明四边形为平行四边形，从而，且，可得为异面直线与所成角（或补角），再利用余弦定理可得结果.

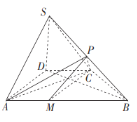
（1）连接，，因为点在以为直径的圆上，所以.

因为，所以，.

所以.

因为为等腰梯形，，

所以.

又因为，，

所以，从而得.

又因为平面平面，平面平面，

所以平面.

（2）由（1）得，

设，则，

所以，解得，

即点是线段的中点.

取的中点为，连接，则由（1）及条件得，且，

所以四边形为平行四边形，从而，且，

所以为异面直线与所成角（或补角）.

因为，所以.

因为，所以，

所以，

所以，

即异面直线与所成角的余弦值为.