题目内容
13.设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则f(1)=4.分析 由切线方程可得g(1)=3,可得f(1)=g(1)+1,即可得到所求值.
解答 解:曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,
可得g(1)=3,g′(1)=2,
则f(1)=g(1)+1=3+1=4.
故答案为:4.
点评 本题考查导数的运用:求切线的斜率,考查函数值的求法,注意运用代入法,考查运算能力,属于基础题.

练习册系列答案
相关题目
1.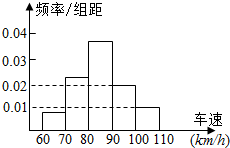 在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )
在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )
 在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )
在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )| A. | 12辆 | B. | 80辆 | C. | 100辆 | D. | 120辆 |
8.某蔬菜基地于2015年4月5日让一批西红柿进入市场销售,通过市场调查,预测西红柿的价格f(x)(单位:元/kg)与时间x(x表示距4月5日的天数,单位:天,x∈(0,8])的数据如表所示:
根据上表数据,从下列函数中选取一个函数描述西红柿价格f(x)与上市时间x的变化关系;f(x)=ax+b,f(x)=ax2+bx+c,f(x)=a•bx,f(x)=a•logbx,其中a≠0,并求出此函数以及西红柿价格的最小值.
| 时间x | 3 | 5 | 7 |
| 价格f(x) | 13 | 5 | 5 |
18.若f(x)=$\left\{\begin{array}{l}-2x-2,x∈({-∞,0})\\{x^2}-2x-1,x∈[0,+∞)\end{array}$,x1≤x2≤x3,且f(x1)=f(x2)=f(x3),则x1+x2+x3的取值的范围是( )
| A. | $[{\frac{3}{2},2})$ | B. | $[{\frac{3}{2},2}]$ | C. | $({-\frac{1}{2},1}]$ | D. | $[{\frac{1}{2},2})$ |
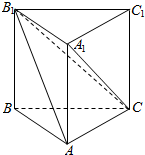 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2.