题目内容
已知函数f（x）=
+1（a＞0，a≠1，b∈R）是奇函数，且f（2）=
．
（1）求a，b的值；
（2）用定义证明f（x）在区间（0，+∞）上是减函数．
| b |
| ax-1 |
| 5 |
| 3 |
（1）求a，b的值；
（2）用定义证明f（x）在区间（0，+∞）上是减函数．
考点：函数单调性的判断与证明,函数奇偶性的判断
专题：函数的性质及应用
分析：（1）根据函数的奇偶性的性质以及（2）=
，建立方程关系即可求出a，b的值．
（2）根据定义法即可证明函数单调性．
| 5 |
| 3 |
（2）根据定义法即可证明函数单调性．
解答：
解：（1）因为f(2)=
+1=
，
所以
=
①，
因为函数f（x）是奇函数，
所以f(-2)=
+1=-f(2)=-
，
所以
=-
②，
由①②可得a=±2（a=-2舍去），所以a=2，b=2．
（2）由（1）可得f(x)=
+1，
设0＜x1＜x2＜+∞，
则f(x1)-f(x2)=(
+1)-(
+1)=
=
因为0＜x1＜x2＜+∞，且y=2x在（0，+∞）为增函数，
所以2x1-1＞0，2x2-1＞0，2x2+1＞2x1+1
所以
＞0，
所以f（x1）＞f（x2），
所以f（x）在区间（0，+∞）上是减函数．
| b |
| a2-1 |
| 5 |
| 3 |
所以
| b |
| a2-1 |
| 2 |
| 3 |
因为函数f（x）是奇函数，
所以f(-2)=
| b |
| a-2-1 |
| 5 |
| 3 |
所以
| ba2 |
| 1-a2 |
| 8 |
| 3 |
由①②可得a=±2（a=-2舍去），所以a=2，b=2．
（2）由（1）可得f(x)=
| 2 |
| 2x-1 |
设0＜x1＜x2＜+∞，
则f(x1)-f(x2)=(
| 2 |
| 2x1-1 |
| 2 |
| 2x2-1 |
| 2(2x2-1)-2(2x1-1) |
| (2x1-1)(2x2-1) |
| 2x2+1-2x1+1 |
| (2x1-1)(2x2-1) |
因为0＜x1＜x2＜+∞，且y=2x在（0，+∞）为增函数，
所以2x1-1＞0，2x2-1＞0，2x2+1＞2x1+1
所以
| 2x2+1-2x1+1 |
| (2x1-1)(2x2-1) |
所以f（x1）＞f（x2），
所以f（x）在区间（0，+∞）上是减函数．
点评：本题主要考查函数奇偶性和单调性的判断和应用，要求熟练掌握函数的性质及其应用．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
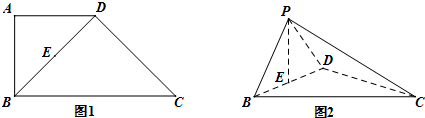
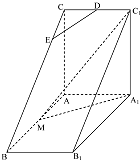如图，直三棱柱ABC=A1B1C1中，AC⊥AB，AB=2AA1，M是AB的中点，△A1MC1是等腰三角形，D为CC1的中点，E为BC上一点且
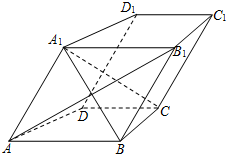如图，在四棱柱ABCD-A1B1C1D1中，AB1⊥BC，AB∥CD，BC⊥AB且AA1=AB=AD=2，∠A1AB=∠DAB=60°．
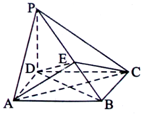如图，在四棱椎P-ABCD中，PD⊥平面ABCD，四边形ABCD是边长为2的菱形，∠ABC=