题目内容
14.一个样本a,99,b,101,c中5个数恰好构成等差数列,则这个样本的标准差为$\sqrt{2}$.分析 设公差为d,则99+2d=101,解得d=1,由此分别求出a,b,c,从而求出这个样本的平均数,由此能求出这个样本的标准差.
解答 解:∵一个样本a,99,b,101,c中5个数恰好构成等差数列,
设公差为d,则99+2d=101,解得d=1,
∴a=99-1=98,b=99+1=100,c=101+1=102,
∴这个样本的平均数$\overline{x}$=$\frac{1}{5}$(98+99+100+101+102)=100,
这个样本的方差S2=$\frac{1}{5}$[(-2)2+(-1)2+02+12+22]=2,
∴这个样本的标准差为$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查样本数据的标准差的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
12.将曲线$y=2sin(x+\frac{π}{3})$上所有点的横坐标伸长为原来的3倍,纵坐标不变,得到的曲线方程为( )
| A. | $y=2sin(3x+\frac{π}{3})$ | B. | y=2sin(3x+π) | C. | $y=2sin(\frac{1}{3}x+\frac{π}{3})$ | D. | $y=2sin(\frac{1}{3}x+\frac{π}{9})$ |
5.已知正项等比数列{an}的前n项和为Sn,且4a2=a4,则$\frac{S_4}{{{a_2}+{a_5}}}$等于( )
| A. | $\frac{5}{6}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{9}$ |
2.函数y=tanx(-$\frac{π}{4}$≤x≤$\frac{π}{4}$且x≠0)的值域是( )
| A. | [-1,1] | B. | [-1,0)∪(0,1] | C. | (-∞,1] | D. | [-1,+∞) |
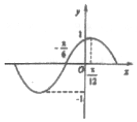 函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.
函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.