题目内容
P为函数y=ex图象上的点,则点P到直线y=x的最短距离为( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:利用导数研究曲线上某点切线方程,点到直线的距离公式
专题:导数的综合应用
分析:根据函数y=ex,利用导数求出切点坐标,利用点到直线的距离求解即可.
解答:
解:设曲线y=ex上斜率为1的切线为y=x+b,
∵y′=ex,由ex=1得x=0,
即切点为(0,1),
∴d=
=
,
∴P、Q两点间的最短距离为:
,
故选:C.
∵y′=ex,由ex=1得x=0,
即切点为(0,1),
∴d=
| 1 | ||
|
| ||
| 2 |
∴P、Q两点间的最短距离为:
| ||
| 2 |
故选:C.
点评:本题考查导数的几何意义,点到直线的距离公式等式知识的灵活应用,属于中档题.

练习册系列答案
相关题目
已知非零向量
,
满足|
-
|=|
+
|=λ|
|(λ≥2),则
-
与
+
的夹角的取值范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
A、(0,
| ||
B、(0,
| ||
C、[0,
| ||
D、[
|
执行如图所示的程序框图,若输入x=1,则输出y的值为( )


| A、5 | B、122 | C、14 | D、41 |
 定义在R上的函数f(x)满足f(4)=1,已知f(x)的导函数f(x)′的图象如图所示,若两个正数a、b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1,已知f(x)的导函数f(x)′的图象如图所示,若两个正数a、b满足f(2a+b)<1,则| a+2b+3 |
| a+1 |
A、(
| ||||
B、(-∞,
| ||||
C、(
| ||||
| D、(-∞,3) |
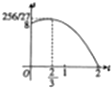
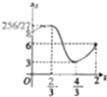
 如图是一块不规则的铁皮,已知AB⊥BC,OA∥BC,AB=PC=2OA=4,曲线段OC是以点O为顶点,且开口向右的抛物线的一段,现用这块铁皮截出一块矩形铁皮,其中矩形的一对邻边分别在AB、BC上,且一个顶点P落在曲线段OC上,设点P到直线AB的距离为t+2,所截矩形铁皮的面积为S,则函数S=f(t)的图象大致是( )
如图是一块不规则的铁皮,已知AB⊥BC,OA∥BC,AB=PC=2OA=4,曲线段OC是以点O为顶点,且开口向右的抛物线的一段,现用这块铁皮截出一块矩形铁皮,其中矩形的一对邻边分别在AB、BC上,且一个顶点P落在曲线段OC上,设点P到直线AB的距离为t+2,所截矩形铁皮的面积为S,则函数S=f(t)的图象大致是( )