题目内容
5.设数列{an}满足a1=6,a2=-3,2an+2=an+1+an.(1)记bn=an+1-an,证明:{bn}是等比数列;
(2)求数列{an}的前n项和Sn的最大值和最小值.
分析 (1)利用2an+2=an+1+an,bn=an+1-an,即可证明{bn}是以-9为首项,-$\frac{1}{2}$为公比的等比数列;
(2)由(1)可知bn=$-9•(-\frac{1}{2})^{n-1}$,求出数列{an}的通项、前n项和Sn,即可求出最大值和最小值.
解答 (1)证明:∵2an+2=an+1+an,bn=an+1-an,
∴bn+1=-$\frac{1}{2}$bn,
∵a1=6,a2=-3,∴b1=-9,
∴{bn}是以-9为首项,-$\frac{1}{2}$为公比的等比数列;
(2)解:由(1)可知bn=$-9•(-\frac{1}{2})^{n-1}$,
∴an=b1+b2+…+bn-1+a1=$6×(-\frac{1}{2})^{n-1}$,
∴数列{an}的前n项和Sn=6×$\frac{1-(-\frac{1}{2})^{n}}{1+\frac{1}{2}}$,
∴数列{an}的前n项和Sn的最大值为6,最小值为3.
点评 本题考查数列递推式,考查数列的通项与求和,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
17.在等腰直角△ABC中,∠ABC=90°,AB=BC=2,M,N(不与A,C重合)为AC边上的两个动点,且满足|$\overrightarrow{MN}$|=$\sqrt{2}$,则$\overrightarrow{BM}$•$\overrightarrow{BN}$的取值范围为( )
| A. | [$\frac{3}{2}$,2] | B. | ($\frac{3}{2}$,2) | C. | [$\frac{3}{2}$,2) | D. | [$\frac{3}{2}$,+∞) |
14.如图,该程序运行后输出的结果是( )


| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
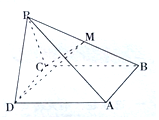 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.