题目内容
3.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线分别交于A,B两点,O为坐标原点,若双曲线的离心率为2,则△AOB的面积为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
分析 求出双曲线的渐近线方程,抛物线的准线方程x=-1,解得交点A,B,运用离心率公式和a,b,c的关系,化简即可得到求得三角形的面积.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线方程为y=±$\frac{b}{a}$x,
抛物线y2=4x的准线为x=-1,
可得A(-1,$\frac{b}{a}$),B(-1,-$\frac{b}{a}$),
即有△AOB的面积为$\frac{1}{2}$•1•$\frac{2b}{a}$=$\frac{b}{a}$,
由e=$\frac{c}{a}$=2,即c=2a,
b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$a,
则△AOB的面积为$\frac{b}{a}$=$\sqrt{3}$.
故选:D.
点评 本题考查双曲线的方程和性质,主要是渐近线方程和离心率公式的运用,同时考查抛物线的准线方程,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的一个焦点F作双曲线的一条渐近线的垂线,若垂线的延长线与y轴的交点坐标为$(0\;,\;\;\frac{c}{2})$,则此双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
18.已知点A为双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)上任意一点,且它到双曲线的两条渐近线的距离之积为定值3,则$\frac{1}{a^2}$+$\frac{1}{b^2}$=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |
8.过抛物线y2=2px(p>0)的焦点F,且倾斜角为$\frac{π}{4}$的直线与抛物线交于A,B两点,若AB的垂直平分线经过点(0,2),M为抛物线上的一个动点,则M到直线11:5x-4y+4=0和l2:x=-$\frac{2}{5}$的距离之和的最小值为( )
| A. | $\frac{6\sqrt{41}}{41}$ | B. | $\frac{6\sqrt{31}}{31}$ | C. | $\frac{3\sqrt{41}}{41}$ | D. | $\frac{3\sqrt{31}}{31}$ |
15.已知抛物线C:y2=4x,直线l交C于A,B两点,O为坐标原点,直线OA,OB的斜率分别为k1,k2,若k1•k2=-2,则△AOB面积的最小值为( )
| A. | 4 | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
13.已知两个命题:
p:“若复数z1,z2满足z1-z2>0,则z1>z2.”;
q:“存在唯一的一个实数对(a,b)使得a-bi=i(2+i).”
其真假情况是( )
p:“若复数z1,z2满足z1-z2>0,则z1>z2.”;
q:“存在唯一的一个实数对(a,b)使得a-bi=i(2+i).”
其真假情况是( )
| A. | p真q假 | B. | p假q假 | C. | p假q真 | D. | p真q真 |
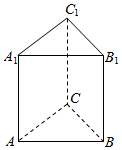 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=AC=2,AA1=4
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=AC=2,AA1=4