题目内容
14.已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=xa(a∈R),函数f(x)的图象经过点(4,2).(1)求函数f(x)的解析式;
(2)解不等式f(x2)-f(-x2+x-1)>0.
分析 (1)根据函数f(x)的图象经过点(4,2).可得a值,结合f(x)是定义在R上的偶函数,可得函数的解析式;
(2)不等式f(x2)-f(-x2+x-1)>0可化为:|x2|>|-x2+x-1|,即x2>x2-x+1,解得答案.
解答 解:(1)∵函数f(x)的图象经过点(4,2).
∴4a=2,解得:a=$\frac{1}{2}$,
故当x≥0时,f(x)=$\sqrt{x}$,
当x<0时,-x>0,
由f(x)是定义在R上的偶函数,可得此时f(x)=f(-x)=$\sqrt{-x}$,
综上可得:f(x)=$\sqrt{\left|x\right|}$
(2)若f(x2)-f(-x2+x-1)>0,
则f(x2)>f(-x2+x-1),
则|x2|>|-x2+x-1|,
即x2>x2-x+1,
解得:x>1
点评 本题考查的知识点是函数奇偶性性质,不等式的解法,函数解析式的求法,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知sin(α-β)=-$\frac{12}{13}$,cosβ=-$\frac{4}{5}$,且α-β∈(π,$\frac{3π}{2}$),β∈($\frac{π}{2}$,π),求sinα.
18.若点M在直线l上,l在平面α内,则M,l,α间的上关系为( )
| A. | M∈l,l∈α | B. | M∈l,l?α | C. | M?l,l?α | D. | M?l,l∈α |
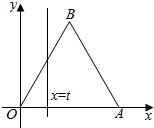 如图,△OAB是边长为2的正三角形,当一条垂直于底边OA(垂足不与O,A重合)的直线x=t从左至右移动时,直线l把三角形分成两部分,记直线l左边部分的面积y.
如图,△OAB是边长为2的正三角形,当一条垂直于底边OA(垂足不与O,A重合)的直线x=t从左至右移动时,直线l把三角形分成两部分,记直线l左边部分的面积y.