题目内容
已知A(1,0),B(0,1),C(3,4)
(1)求△ABC外接圆的方程
(2)以(3,1)为中点的弦EF所在的直线l交坐标轴于M,N,求△OMN的面积.
(1)求△ABC外接圆的方程
(2)以(3,1)为中点的弦EF所在的直线l交坐标轴于M,N,求△OMN的面积.
考点:圆的标准方程,直线与圆的位置关系
专题:直线与圆
分析:(1)设△ABC外接圆的方程为x2+y2+Dx+Ey+F=0,把A(1,0),B(0,1),C(3,4)代入,能求出△ABC外接圆的方程.
(2)△ABC外接圆的圆心为P(2,2),设弦EF中点Q(3,1),所以PQ⊥EF,由此能求出△OMN的面积.
(2)△ABC外接圆的圆心为P(2,2),设弦EF中点Q(3,1),所以PQ⊥EF,由此能求出△OMN的面积.
解答:
解:(1)设△ABC外接圆的方程为x2+y2+Dx+Ey+F=0,
已知A(1,0),B(0,1),C(3,4)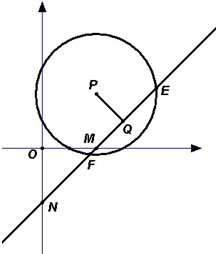
∴
,
解得D=-4,E=-4,F=3,
∴△ABC外接圆的方程为x2+y2-4x-4y+3=0,
即(x-2)2+(y-2)2=5.
(2)△ABC外接圆的圆心为P(2,2),设弦EF中点Q(3,1),
所以PQ⊥EF,
∵kPQ=
=-1,∴kEF=
=1,
∴直线EF的方程为y-1=x-3,即x-y-2=0,
∵直线EF与坐标轴交于M,N两点,
∴M(0,-2),N(2,0),如图,
△OMN的面积为
|OM||ON|=
×2×2=2.
已知A(1,0),B(0,1),C(3,4)

∴
|
解得D=-4,E=-4,F=3,
∴△ABC外接圆的方程为x2+y2-4x-4y+3=0,
即(x-2)2+(y-2)2=5.
(2)△ABC外接圆的圆心为P(2,2),设弦EF中点Q(3,1),
所以PQ⊥EF,
∵kPQ=
| 2-1 |
| 2-3 |
| 1 |
| kPQ |
∴直线EF的方程为y-1=x-3,即x-y-2=0,
∵直线EF与坐标轴交于M,N两点,
∴M(0,-2),N(2,0),如图,
△OMN的面积为
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查圆的方程的求法,考查三角形的面积的求法,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
知f(x)是实数集上的偶函数,且在区间[0,+∞)上是增函数,则f(-2),f(-π),f(3)的大小关系是( )
| A、f(-π)>f(-2)>f(3) |
| B、f(3)>f(-π)>f(-2) |
| C、f(-2)>f(3)>f(-π) |
| D、f(-π)>f(3)>f(-2) |
观察下列各式:55=3125,56=15625,57=78125,58=390625,59=1953125则52012的末四位数字为( )
| A、3125 | B、5625 |
| C、0625 | D、8125 |

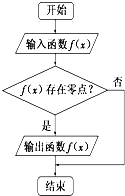 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数: