题目内容
已知全集U=R,A={x|
<-1},非空集合B={x|x2-3(a+1)x+2(3a+1)≤0}.
(1)当a=2时,求(∁UA)∩B:
(2)命题p:x∈A,命题q:x∈B,若p是q的必要条件,求实数a的取值范围.
| 3 |
| x-4 |
(1)当a=2时,求(∁UA)∩B:
(2)命题p:x∈A,命题q:x∈B,若p是q的必要条件,求实数a的取值范围.
考点:必要条件、充分条件与充要条件的判断,交、并、补集的混合运算
专题:简易逻辑
分析:(1)当a=2时,求出集合B,根据集合的基本运算即可求(∁UA)∩B:
(2)根据命题充分条件和必要条件的定义和关系,即可求实数a的取值范围.
(2)根据命题充分条件和必要条件的定义和关系,即可求实数a的取值范围.
解答:
解:(1)A={x|
<-1}={x|
+1=
<0}={x|1<x<4},
当a=2时,B={x|x2-3(a+1)x+2(3a+1)≤0}={x|x2-9x+14≤0}={x|2≤x≤7}.
则∁UA={x|x≥4或x≤1},
则(∁UA)∩B={x|4≤x≤7}.
(2)∵p是q的必要条件,
∴B⊆A,
由B={x|x2-3(a+1)x+2(3a+1)≤0}={x|(x-2)[x-(3a+1)]≤0}.
①若3a+1≥2,即a≥
,此时B={x|2≤x≤3a+1}
∵A={x|1<x<4},B⊆A,
∴此时满足3a+1<4,即
≤a<1,
②若3a+1<2,即a<
,此时B={x|3a+1≤x≤2}
∵A={x|1<x<4},B⊆A,
∴此时满足3a+1≥1,即0≤a<
,
综上0≤a<1,
即实数a的取值范围0≤a<1.
| 3 |
| x-4 |
| 3 |
| x-4 |
| x-1 |
| x-4 |
当a=2时,B={x|x2-3(a+1)x+2(3a+1)≤0}={x|x2-9x+14≤0}={x|2≤x≤7}.
则∁UA={x|x≥4或x≤1},
则(∁UA)∩B={x|4≤x≤7}.
(2)∵p是q的必要条件,
∴B⊆A,
由B={x|x2-3(a+1)x+2(3a+1)≤0}={x|(x-2)[x-(3a+1)]≤0}.
①若3a+1≥2,即a≥
| 1 |
| 3 |
∵A={x|1<x<4},B⊆A,
∴此时满足3a+1<4,即
| 1 |
| 3 |
②若3a+1<2,即a<
| 1 |
| 3 |
∵A={x|1<x<4},B⊆A,
∴此时满足3a+1≥1,即0≤a<
| 1 |
| 3 |
综上0≤a<1,
即实数a的取值范围0≤a<1.
点评:本题主要考查集合的基本运算以及充分条件和必要条件的应用,利用不等式的性质是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知偶数f(x)以4为周期,且当x∈[-2,0]时,f(x)=(
)x-1,若在区间[-6,6]内关于x的方程f(x)•log2(|x|+2)=0(a>1)恰有4个不同的实数根,则a的取值范围是( )
| 1 |
| 2 |
| A、(1,2) | |||
| B、(2,+∞) | |||
C、(1,
| |||
D、(
|
已知sin(α-
)=
,且α为锐角,则cosα=( )
| π |
| 4 |
| 3 |
| 5 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
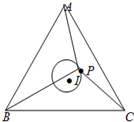 设等边三角形ABC的边长为4
设等边三角形ABC的边长为4| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|