题目内容
已知数列{an}满足:an+2an-an+1=tn(t-1),a1=1,a2=t(t>1,t为常数)
(1)求a3;
(2)求证:an+1>an≥1;
(3)求证:{an}满足an+2-2tan+1+tan=0.
(1)求a3;
(2)求证:an+1>an≥1;
(3)求证:{an}满足an+2-2tan+1+tan=0.
考点:数列递推式,数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(1)由a3a1-a22=t(t-1)和a1=1,a2=t,能求出a3.
(2)由t>1知:an+2an>an+12≥0,所以an+2an>0,故an+2与an同号,由此能够证明an+1>an≥1.
(3)由an+2an-an+12=tn(t-1),(n∈N*)得an+1an-1-an2=tn-1(t-1)(n≥2),所以an+2an-an+12=tan+1an-1-tan2,
=
,由此能够证明an+2-2tan+1+tan=0.
(2)由t>1知:an+2an>an+12≥0,所以an+2an>0,故an+2与an同号,由此能够证明an+1>an≥1.
(3)由an+2an-an+12=tn(t-1),(n∈N*)得an+1an-1-an2=tn-1(t-1)(n≥2),所以an+2an-an+12=tan+1an-1-tan2,
| an+2+tan |
| an+1 |
| an+1+tan-1 |
| an |
解答:
(1)解:由a3a1-a22=t(t-1)和a1=1,a2=t
∴a3=2t2-t;
(2)证明:由t>1知:an+2an>an+12≥0
∴an+2an>0
故an+2与an同号
而a1=1>0,a2=t>0.故an>0.
又an+2an>an+12,
即
>
∴
>
>…>
=t>1
∴an+1>an
∴an≥1
∴an+1>an≥1;
(3)证明:由an+2an-an+12=tn(t-1),(n∈N*)
得an+1an-1-an2=tn-1(t-1)(n≥2),
再由上两式相除得到:∴an+2an-an+12=tan+1an-1-tan2
∴an(an+2+tan)=an+1(an+1+tan-1),
∴
=
,
即{
}为常数列,
∴
=
,
而a3+ta1=2t2,∴
=2t.
即an+2-2tan+1+tan=0.
∴a3=2t2-t;
(2)证明:由t>1知:an+2an>an+12≥0
∴an+2an>0
故an+2与an同号
而a1=1>0,a2=t>0.故an>0.
又an+2an>an+12,
即
| an+2 |
| an+1 |
| an+1 |
| an |
∴
| an+1 |
| an |
| an |
| an-1 |
| a2 |
| a1 |
∴an+1>an
∴an≥1
∴an+1>an≥1;
(3)证明:由an+2an-an+12=tn(t-1),(n∈N*)
得an+1an-1-an2=tn-1(t-1)(n≥2),
再由上两式相除得到:∴an+2an-an+12=tan+1an-1-tan2
∴an(an+2+tan)=an+1(an+1+tan-1),
∴
| an+2+tan |
| an+1 |
| an+1+tan-1 |
| an |
即{
| an+2+tan |
| an+1 |
∴
| an+2+tan |
| an+1 |
| a3+ta1 |
| a2 |
而a3+ta1=2t2,∴
| an+2+tan |
| an+1 |
即an+2-2tan+1+tan=0.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意不等式性质的合理运用.

练习册系列答案
相关题目
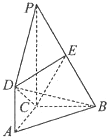 如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.
如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.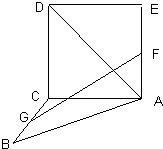 如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点.求AD与GF所成的角的余弦值.
如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点.求AD与GF所成的角的余弦值.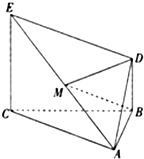 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=2BD,M是EA的中点
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=2BD,M是EA的中点 如图:已知长方体ABCD-A1B1C1D1的底面ABCD是边长为2的正方形,高AA1=2
如图:已知长方体ABCD-A1B1C1D1的底面ABCD是边长为2的正方形,高AA1=2