题目内容

已知x，y，z∈R，且x+2y+3z+8=0．求证：（x-1）2+（y+2）2+（z-3）2≥14．
考点：二维形式的柯西不等式
专题：证明题,不等式
分析：由柯西不等式，可得：[（x-1）2+（y+2）2+（z-3）2]（12+22+32）≥[（x-1）+（y+2）+（z-3）]2=（x+2y+3z-6）2，即可得出结论．
解答： 证明：因为：[（x-1）2+（y+2）2+（z-3）2]（12+22+32）≥[（x-1）+（y+2）+（z-3）]2
=（x+2y+3z-6）2=142，…（8分）
当且仅当
x-1
1
=
y+2
2
=
z-3
3
，即x=z=0，y=-4时，取等号，
所以：（x-1）2+（y+2）2+（z-3）2≥14．                    …（10分）
点评：此题主要考查一般形式的柯西不等式的应用，考查学生分析解决问题的能力．
练习册系列答案
相关题目
已知函数f（x）=x2+2alnx．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若函数g（x）=
2
x
+f（x）在[1，2]上是减函数，求实数a的取值范围．
如图，已知△ASD中，SD=3，CD=
5
，cos∠SDC=-
1
5
5
，SA=2AD，AB⊥SD交SC于B，M为SB上点，且SM=2MB，将△SAB沿AB折起，使平面SAB⊥平面ABCD

（Ⅰ）求证：AM∥平面SCD；
（Ⅱ）求三棱锥S-CDM的体积．
已知在平面直角坐标系xOy中，圆M的方程为（x-4）2+y2=1．以原点O为极点，以x轴正半轴为极轴，且与直角坐标系取相同的单位长度，建立极坐标系，直线l的极坐标方程为ρsin（θ+
π
6
）=
1
2
．
（Ⅰ）求直线l的直角坐标方程和圆M的参数方程；
（Ⅱ）求圆M上的点到直线l的距离的最小值．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）过点（1，
2
2
）和（
2
2
，
3
2
），其中e为椭圆的离心率．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设Q（x0，y0）（x0y0≠0）为椭圆C上一点，取点A（0，
2
），E（x0，0），连接AE，过点A作AE的垂线交x轴于点D．点G是点D关于原点的对称点．证明：直线QG与椭圆C只有一个公共点．
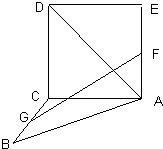如图，正方形ACDE与等腰直角△ACB所在的平面互相垂直，且AC=BC=2，∠ACB=90°，F、G分别是线段AE、BC的中点．求AD与GF所成的角的余弦值．
求函数y=
2x2-2x+1
x2
（x＞2）的值域．
若x∈[-π，π]，为使方程sinx-
3
cosx=q．
（1）有解；
（2）有两个不同的解；
（3）仅有一解；
请分别求q的值．
在数列{an}中，已知a1=20，a2=30，an+1=3an-an-1（n∈N*，n≥2）．
（1）当n=2，3时，分别求an2-an-1an+1的值，判断an2-an-1an+1是否为定值，并给出证明；
（2）求出所有的正整数n，使得5an+1an+1为完全平方数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网