题目内容
某工厂某种产品的年固定成本为250万元，每生产x千件需另投入成本为G（x），当年产量不足80千克时，
G（x）=
x2+10x（万元）．当年产量不小于80千件时，G（x）=51x+
-1450（万元）．每件商品售价为0.05万元．通过市场分析，该厂生产的商品能全部售完．则该厂在这一商品的生产中所获年利润的最大值是（ ）
G（x）=
| 1 |
| 3 |
| 10000 |
| x |
| A、900万元 |
| B、950万元 |
| C、1000万元 |
| D、1150万元 |
考点：函数模型的选择与应用
专题：计算题,应用题,不等式的解法及应用
分析：由题意，每千件商品售价为50万元；设该厂生产了x千件商品并全部售完，则所获得的利润为y万元；从而由分段函数求函数的最大值．
解答：
解：由题意，每千件商品售价为50万元；
设该厂生产了x千件商品并全部售完，则所获得的利润为y万元；
则当x＜80时，
y=50x-（
x2+10x）-250
=-
x2+40x-250，
则当x=60时，ymax=950万元；
当x≥80时，
y=50x-（51x+
-1450）-250
=-（x+
）+1200
≤1000；
（当且仅当x=100时，等号成立）；
故该厂在这一商品的生产中所获年利润的最大值是1000万元；
故选C．
设该厂生产了x千件商品并全部售完，则所获得的利润为y万元；
则当x＜80时，
y=50x-（
| 1 |
| 3 |
=-
| 1 |
| 3 |
则当x=60时，ymax=950万元；
当x≥80时，
y=50x-（51x+
| 10000 |
| x |
=-（x+
| 10000 |
| x |
≤1000；
（当且仅当x=100时，等号成立）；
故该厂在这一商品的生产中所获年利润的最大值是1000万元；
故选C．
点评：本题考查了分段函数在实际问题中的应用，同时考查了基本不等式在求最值中的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
设集合M={0，3}，N={1，2，3}，则M∪N=（ ）
| A、{3} |
| B、{0，1，2} |
| C、{1，2，3} |
| D、{0，1，2，3} |
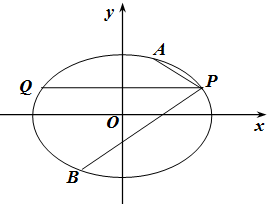已知椭圆C的中心在原点，焦点在x轴上，离心率为