题目内容

复利是一种计算利息的方法，即把前一期的利息和本金加在一起算做本金，再计算下一期的利息．现有一种储蓄按复利计算利息，本金为a元，每期利率为r，设本利和为y，存期为x，则y随着x变化的函数式
 
．
考点：函数解析式的求解及常用方法
专题：应用题
分析：由本金加上本金乘以每期的利率为一期后的本利和，依次可以求得存期为x的本利和．
解答： 解：∵本金为a元，每期利率为r，则1期后的本利和为a+ar=a（1+r），
2期后的本利和为a（1+r）+a（1+r）r=a（1+r）2，
…
x期后的本利和为y=a（1+r）x，x∈N*．
故答案为：y=a（1+r）x，x∈N*．
点评：本题考查了函数解析式的求解及常用方法，体现了简单的数学建模思想方法，关键是对复利的理解与运用，是基础题．
练习册系列答案
相关题目
如图，半径为R的半圆内的阴影部分以直径AB所在直线为轴，旋转一周得到一几何体，求该几何体的体积，（其中∠BAC=30°）
如图，设D是边长为l的正方形区域，E是D内函数y=
x
与y=x2所构成（阴影部分）的区域，在D中任取一点，则该点在E中的概率是（　　）
A、
1
3
B、
2
3
C、
1
6
D、
1
4
行列式
.
3
Acosx
A
2
-2Asinx0
11cosx
.
（A＞0）按第一列展开得
3
M11-2M21+M31，记函数f（x）=M11+M21，且f（x）的最大值是4．
（1）求A；
（2）将函数y=f（x）的图象向左平移
π
12
个单位，再将所得图象上各点的横坐标扩大为原来的2倍，纵坐标不变，得到函数y=g（x）的图象，求g（x）在(-
π
12
，
11π
12
)上的值域．
在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．曲线C1的参数方程为
x=
t
y=t+1
（t为参数），曲线C2的极坐标方程为
2
ρsin（θ-
π
4
）=3，则C1与C2交点在直角坐标系中的坐标为
 
．
一个几何体的三视图如图所示，则这个几何体的体积是（　　）
A、1
B、2
C、
2
3
D、
1
3
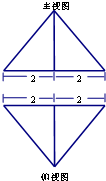三棱锥P-ABC的主视图和俯视图为如图所示的两个全等的等腰三角形，其中底边长为4，腰长为3，则该三棱锥左视图的面积为（　　）
A、
5
2
B、2
5
C、
5
D、5
（Ⅰ）若a是从1，2，3，4四个数中任取的一个数，b是从1，2，3三个数中任取的一个数，求点P（a，b）在椭圆
x2
16
+
y2
9
=1内的概率．
（Ⅱ）若a是从区间（0，3]任取的一个实数，b是从区间（0，3]任取的一个实数，求直线y=x+1与椭圆
x2
a2
+
y2
b2
=1有公共点的概率．
若函数f（x）=2x-mx在区间（-1，0）内有一个零点，则实数m的取值可以是（　　）
A、-1
B、1
C、．-
1
4
D、
1
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网