题目内容
8.某四棱锥的三视图如图所示,该四棱锥的表面积是( )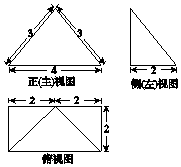
| A. | 20+2$\sqrt{5}$ | B. | 14+4$\sqrt{5}$ | C. | 26 | D. | 12+2$\sqrt{5}$ |
分析 由三视图得几何体是四棱锥并画出直观图,由三视图判断出线面的位置关系,并求出几何体的高和侧面的高,分别求出各个侧面和底面的面积,即可得到答案.
解答 解:由三视图得几何体是四棱锥P-ABCD, 如图所示:
如图所示:
且PE⊥平面ABCD,底面ABCD是矩形,AB=4、AD=2,
面PDC是等腰三角形,PD=PC=3,
则△PDC的高为$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
所以△PDC的面积为:$\frac{1}{2}$×4×$\sqrt{5}$=2$\sqrt{5}$,
因为PE⊥平面ABCD,所以PE⊥BC,
又CB⊥CD,PE∩CD=E,所以BC⊥面PDC,
即BC⊥PC,同理可证AD⊥PD,
则两个侧面△PAD、△PBC的面积都为:$\frac{1}{2}$×2×3=3,
侧面△PAB的面积为:$\frac{1}{2}$×4×$\sqrt{(\sqrt{5})^{2}+{2}^{2}}$=6,且底面ABCD的面积为:4×2=8,
所以四棱锥P-ABCD的表面积S=2$\sqrt{5}$+2×3+6+8=20+2$\sqrt{5}$,
故选A.
点评 本题考查由三视图求几何体的表面积,由三视图正确复原几何体、判断出几何体的结构特征是解题的关键,考查空间想象能力.

练习册系列答案
相关题目
18.在平行四边形ABCD中,若$|{\overrightarrow{AB}-\overrightarrow{AD}}|=|{\overrightarrow{AB}+\overrightarrow{AD}}|$,则平行四边形ABCD是( )
| A. | 矩形 | B. | 梯形 | C. | 正方形 | D. | 菱形 |
17.已知平面向量$\overrightarrow{a}$=(-1,2)与$\overrightarrow{b}$=(3k-1,1)互相垂直,则k的值为( )
| A. | $\frac{1}{6}$ | B. | 1 | C. | 3 | D. | 6 |
17.lg2+2lg5=( )
| A. | 1+lg5 | B. | 2+lg5 | C. | 2 | D. | 1 |