题目内容
17.已知平面向量$\overrightarrow{a}$=(-1,2)与$\overrightarrow{b}$=(3k-1,1)互相垂直,则k的值为( )| A. | $\frac{1}{6}$ | B. | 1 | C. | 3 | D. | 6 |
分析 利用向量垂直的性质直接求解.
解答 解:∵平面向量$\overrightarrow{a}$=(-1,2)与$\overrightarrow{b}$=(3k-1,1)互相垂直,
∴$\overrightarrow{a}•\overrightarrow{b}$=-1×(3k-1)+2×1=0,
解得k=1.
故选:B.
点评 本题考查实数值的求法,是基础题,解题时要 认真审题,注意向量垂直的性质的合理运用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
8.某四棱锥的三视图如图所示,该四棱锥的表面积是( )
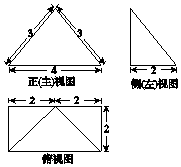

| A. | 20+2$\sqrt{5}$ | B. | 14+4$\sqrt{5}$ | C. | 26 | D. | 12+2$\sqrt{5}$ |
12.下列命题中,正确的命题是( )
| A. | 平行于同一直线的两个平面平行 | |
| B. | 共点的三条直线只能确定一个平面 | |
| C. | 若一个平面中有无数条直线与另一个平面平行,则这两个平面平行 | |
| D. | 存在两条异面直线同时平行于同一个平面 |
9.抛物线y2=2x的焦点为F,点P在抛物线上,点O为坐标系原点,若|PF|=3,则|PO|等于( )
| A. | $\frac{3\sqrt{5}}{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{5\sqrt{5}}{2}$ | D. | 4$\sqrt{2}$ |
5.执行如图所示的程序框图,则输出S=( )
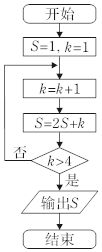

| A. | 26 | B. | 247 | C. | 120 | D. | 57 |
6.正方体的棱长为2$\sqrt{3}$,顶点都在同一球面上,则该球的表面积为( )
| A. | 36π | B. | 72π | C. | 288π | D. | 144π |
 如图,在直三棱柱ABC-A1B1C1中,AC=BC,F为A1B1的中点.求证:
如图,在直三棱柱ABC-A1B1C1中,AC=BC,F为A1B1的中点.求证: