题目内容
14．复数z=（m2-2m-3）+（m2-4m+3）i是纯虚数，实数m=（ ）| A． | 1 | B． | -1 | C． | 1或-3 | D． | -1或3 |
分析 由实部为0且虚部不为0列式求解．
解答 解：∵z=（m2-2m-3）+（m2-4m+3）i是纯虚数，
∴$\left\{\begin{array}{l}{{m}^{2}-2m-3=0}\\{{m}^{2}-4m+3≠0}\end{array}\right.$，解得：m=-1．
故选：B．
点评 本题考查复数的基本概念，考查了一元二次方程的解法，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
5．某几何体的三视图如图所示，若可放入一球于其内部且与其各面相切，则该几何体的表面积为（ ）
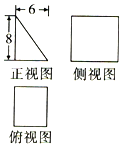
| A． | 96 | B． | 144 | C． | 192 | D． | 240 |
9．设X～B（4，p），其中0＜p＜$\frac{1}{2}$，且P（X=2）=$\frac{8}{27}$，那么P（X=1）=（ ）
| A． | $\frac{8}{81}$ | B． | $\frac{16}{81}$ | C． | $\frac{8}{27}$ | D． | $\frac{32}{81}$ |