某几何体的三视图如图所示.若可放入一球于其内部且与其各面相切.则该几何体的表面积为( )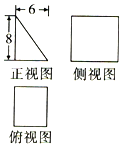A．96B．144C．192D．240 题目和参考答案——青夏教育精英家教网—

题目内容

5．某几何体的三视图如图所示，若可放入一球于其内部且与其各面相切，则该几何体的表面积为（　　）

A．

B．

144

C．

192

D．

240

分析如图，该几何体是底面为直角三角形的直三棱柱，则其内切球半径为底面三角形的内切圆半径$r=\frac{8+6-10}{2}=2$，三棱柱的高等于4，即可求出其表面积．

解答解：如图，该几何体是底面为直角三角形的直三棱柱，则其内切球半径为底面三角形的内切圆半径$r=\frac{8+6-10}{2}=2$，三棱柱的高等于4，
所以其表面积为$\frac{1}{2}×6×8×2+6×4+8×4+10×4=144$，
故选B．

点评本题考查由三视图求面积，考查学生的计算能力，确定直观图的形状是关键．

练习册系列答案

假期乐园寒假北京教育出版社系列答案

寒假作业与生活陕西师范大学出版总社系列答案

新课程寒假作业本山西教育出版社系列答案

16．已知在等腰梯形ABCD中．AB∥CD，AB=2CD，双曲线M以A、B为焦点．且过C、D两点，点E在双曲线M上．若$\overrightarrow{AE}=\frac{2}{5}\overrightarrow{AC}$，则双曲线的离心率为$\frac{8\sqrt{7}}{7}$．

13．已知$f（x）={sin^2}（2x-\frac{π}{4}）-2t•sin（2x-\frac{π}{4}）+{t^2}-6t+1（x∈[\frac{π}{24}，\frac{π}{2}]）$其最小值为g（t）．
（1）若t=1，求$f（{\frac{π}{8}}）$的值；
（2）求g（t）的表达式；
（3）当$-\frac{1}{2}≤t≤1$时，要使关于t的方程g（t）=kt有一个实根，求实数k的取值范围．

20．已知函数$f（x）=ln\frac{1}{2x}-a{x^2}+x$．
（Ⅰ）当a＞0时，讨论函数f（x）的极值点的个数；
（Ⅱ）若f（x）有两个极值点x₁，x₂，证明：f（x₁）+f（x₂）＞3-4ln2．

10．已知圆O：x²+y²=1，一只蚂蚁从点$A（{\frac{1}{2}，-\frac{{\sqrt{3}}}{2}}）$出发，沿圆周爬行（逆时针或顺时针），当它爬行到点B（-1，0）时，蚂蚁爬行的最短路程为（　　）

17．在△ABC中，角A，B，C的对边分别为a，b，c，AH为边BC上的高，有以下结论：
①$\overrightarrow{AC}•\frac{{\overrightarrow{AH}}}{{|{\overrightarrow{AH}}|}}=c\;sinB$；
②$\overrightarrow{BC}•（\overrightarrow{AC}-\overrightarrow{AB}）={b^2}+{c^2}-2bccosA$；
③$\overrightarrow{AH}•\overrightarrow{AC}={\overrightarrow{AH}^2}$；
④$\overrightarrow{AH}•（\overrightarrow{AB}+\overrightarrow{BC}）=\overrightarrow{AH}•\overrightarrow{AB}$．
其中所有的正确序号的是①②③④．

14．复数z=（m²-2m-3）+（m²-4m+3）i是纯虚数，实数m=（　　）

15．设定点F₁（0，2），F₂（0，-2），动点P满足条件$|{P{F_1}}|+|{P{F_2}}|=a+\frac{4}{a}（a＞0）$，则点P的轨迹是（　　）

试题分类